题目内容

用数学归纳法证明1+q+q2+…+qn+1=
qn+2-1
q-1
(q≠1)．在验证n=1等式成立时，等式的左边的式子是（　　）
A．1B．1+qC．1+q+q2D．1+q+q2+q3
观察1+q+q2+…+qn+1=
qn+2-1
q-1
（q≠1），
等式的左端是以1为首项，q为公比的前n+2项和，最后一项为qn+1，
∴验证n=1等式成立时，等式的左边的式子是1+q+q2．
故选C．
练习册系列答案
相关题目
在中,若,则,用类比的方法,猜想三棱锥的类似性质,并证明你的猜想
设f(n)=1+
1
2
+
1
3
+…+
1
n
，是否存在g（n），使等式f（1）+f（2）+…+f（n-1）=g（n）[f（n）-1]对n≥2的一切自然数都成立，并证明你的结论．
（1）用反证法证明：如果x＞
1
2
，那么x2+2x-1≠0；
（2）用数学归纳法证明：
1
1×3
+
1
3×5
+…+
1
(2n-1)×(2n+1)
=
n
2n+1
(n∈N*)．
函数数列{fn（x）}满足：f1（x）=
x
1+x2
（x＞0），fn+1（x）=f1[fn（x）]．
（Ⅰ）求f2（x），f3（x）；
（Ⅱ）猜想fn（x）的解析式，并用数学归纳法证明．
设关于正整数n的函数f（n）=1•22+2•32+…n（n+1）2
（1）求f（1），f（2），f（3）；
（2）是否存在常数a，b，c使得f（n）=
n(n+1)
12
(an2+bn+c)对一切自然数n都成立？并证明你的结论．
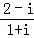（2011•山东）复数z=（i是虚数单位）在复平面内对应的点位于象限为（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
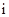已知是虚数单位，若复数是纯虚数，则实数等于.
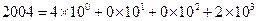在十进制中，那么在5进制中数码2004折合成十进制为                                                           
A．29B．254C．602D．2004

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网