题目内容
(1)用反证法证明:如果x>
,那么x2+2x-1≠0;
(2)用数学归纳法证明:
+
+…+
=
(n∈N*).
| 1 |
| 2 |
(2)用数学归纳法证明:
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| (2n-1)×(2n+1) |
| n |
| 2n+1 |
(1)证明:假设x2+2x-1=0,则x=-1±
,
要证:-1+
<
,只需证:
<
,只需证:2<
上式显然成立,故有-1+
<
.而-1-
<
,
综上,-1+
<
,-1-
<
,都与已知x>
相矛盾,
因此假设不成立,也即原命题成立.
(2)证明:①当n=1时,左边=
,右边=
=
∴n=1时成立,
②假设当n=k(k≥1)时成立,即
+
+…+
=
(k∈N*)
那么当n=k+1时,左边=
+
+…+
+
=
+
=
=
=
∴n=k+1时也成立.
根据①②可得不等式对所有的n≥1都成立.
| 2 |
要证:-1+
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
上式显然成立,故有-1+
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
综上,-1+
| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
因此假设不成立,也即原命题成立.
(2)证明:①当n=1时,左边=
| 1 |
| 1×3 |
| 1 |
| 2×1+1 |
| 1 |
| 3 |
②假设当n=k(k≥1)时成立,即
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| (2k-1)×(2k+1) |
| k |
| 2k+1 |
那么当n=k+1时,左边=
| 1 |
| 1×3 |
| 1 |
| 3×5 |
| 1 |
| (2k-1)×(2k+1) |
| 1 |
| (2k+1)(2k+3) |
=
| k |
| 2k+1 |
| 1 |
| (2k+1)(2k+3) |
| k(2k+3)+1 |
| (2k+1)(2k+3) |
| (2k+)(k+1) |
| (2k+1)(2k+3) |
| k+1 |
| 2k+3 |
∴n=k+1时也成立.
根据①②可得不等式对所有的n≥1都成立.

练习册系列答案
相关题目
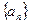 中,
中,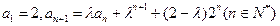 ,其中
,其中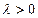 ,求数列
,求数列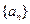 的通项公式
的通项公式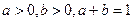 求证:
求证: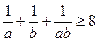 (用两种方法证明).
(用两种方法证明).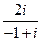 的四个命题:
的四个命题: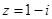 (
(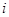 为虚数单位),则复数
为虚数单位),则复数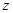 的模
的模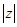 = .
= . ,则
,则

 则正确的结论是( )
则正确的结论是( )


 大小不定
大小不定