题目内容
函数数列{fn(x)}满足:f1(x)=
(x>0),fn+1(x)=f1[fn(x)].
(Ⅰ)求f2(x),f3(x);
(Ⅱ)猜想fn(x)的解析式,并用数学归纳法证明.
| x | ||
|
(Ⅰ)求f2(x),f3(x);
(Ⅱ)猜想fn(x)的解析式,并用数学归纳法证明.
(Ⅰ)∵f1(x)=
(x>0),fn+1(x)=f1[fn(x)],
∴f2(x)=f1[f1(x)]=
=
=
,
f3(x)=f1[f2(x)]=
=
=
,…
(Ⅱ)猜想fn(x)=
.
下面用数学归纳法证明:
1°当n=1时,猜想成立.
2°假设n=k时猜想成立,即有fk(x)=
,
那么fk+1(x)=f1[fk(x)]=
=
=
,
这就是说,当n=k+1时,猜想也成立.
由1°2°可知,猜想对n∈N*均成立.
故fn(x)=
.
| x | ||
|
∴f2(x)=f1[f1(x)]=
| f1(x) | ||
|
| ||||
|
| x | ||
|
f3(x)=f1[f2(x)]=
| f2(x) | ||
|
| ||||
|
| x | ||
|
(Ⅱ)猜想fn(x)=
| x | ||
|
下面用数学归纳法证明:
1°当n=1时,猜想成立.
2°假设n=k时猜想成立,即有fk(x)=
| x | ||
|
那么fk+1(x)=f1[fk(x)]=
| fk(x) | ||
|
| ||||
|
| x | ||
|
这就是说,当n=k+1时,猜想也成立.
由1°2°可知,猜想对n∈N*均成立.
故fn(x)=
| x | ||
|

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 、
、 ,定义
,定义 ,其中
,其中 是
是 、
、 、
、 ,有如下四个命题:
,有如下四个命题: ;
; ;
; ;
; .
.



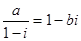 , 其中
, 其中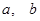 都是实数,
都是实数,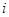 是虚数单位,则
是虚数单位,则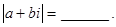
 ,求证:
,求证:
 ,那么z等于( )
,那么z等于( )



 用反证法证明命题“
用反证法证明命题“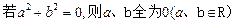 ”,其反设正确的是
”,其反设正确的是


