Question

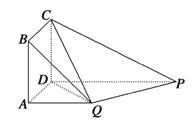
【题目】在平面直角坐标系中，已知矩形的长为2，宽为1，.边分别在轴.轴的正半轴上，点与坐标原点重合（如图所示）。将矩形折叠，使点落在线段上。

（1）若折痕所在直线的斜率为，试求折痕所在直线的方程；

（2）当时，求折痕长的最大值；

（3）当时，折痕为线段，设，试求的最大值。

Answer 1

【答案】（1）；（2）；（3）

【解析】

(1)对k=0,分类讨论，将矩形折叠后点落在线段上的点记为，先求G的坐标，再求折痕所在的直线与的交点坐标，写出直线的点斜式方程.(2) 先求出折痕直线交于点，交轴于，再求的最大值，即得折痕长的最大值.(3)先求得，再求t的表达式和其最大值.

(1) ①当时,此时点与点重合, 折痕所在的直线方程

②当时，将矩形折叠后点落在线段上的点记为，

所以与关于折痕所在的直线对称，

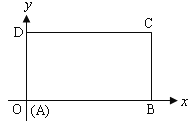
有

故点坐标为，

从而折痕所在的直线与的交点坐标（线段的中点）为

折痕所在的直线方程，即

由①②得折痕所在的直线方程为：

（2）当时，折痕的长为2;

当时，折痕直线交于点，交轴于

∵

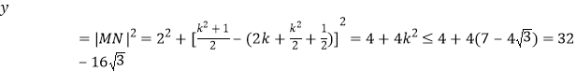
∴折痕长度的最大值为。

而 ,故折痕长度的最大值为

（3）当时，折痕直线交于，交轴于

∵ ∴

∵ ∴（当且仅当时取“=”号）

∴当时，取最大值，的最大值是。