题目内容
17.已知满足条件$\left\{\begin{array}{l}x≥0\\ x+y≤2\\ y≥kx(k>0)\end{array}\right.$的动点(x,y)所在的区域D为一直角三角形区域,则区域D的面积为1.分析 作出平面区域,从而由三角形面积公式求解即可.
解答 解:不等式组$\left\{\begin{array}{l}x-y+1≥0\\ x+y≥1\\ x≤1\end{array}\right.$表示的平面区域如下,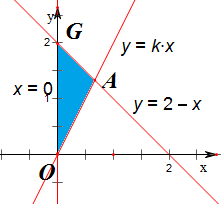
在△OAG中,OG=2,
∵△OAG为直角三角形,
故k=1,则由$\left\{\begin{array}{l}{y=kx}\\{x+y=2}\end{array}\right.$解得,
x=$\frac{2}{1+k}$=1,
故点A到直线OG的距离为1,
故S=$\frac{1}{2}$×1×2=1,
故答案为:1.
点评 本题考查了平面区域的作法与应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.已知点A是抛物线x2=4y的对称轴与准线的交点,点B为抛物线的焦点,P在抛物线上且满足|PA|=m|PB|,当m取最大值时,点P恰好在以A,B为焦点的双曲线上,则双曲线的离心率为( )
| A. | $\frac{\sqrt{2}+1}{2}$ | B. | $\sqrt{2}$+1 | C. | $\frac{\sqrt{5}-1}{2}$ | D. | $\sqrt{5}$-1 |
5.函数y=x-2sinx的图象大致是( )
| A. |  | B. |  | C. |  | D. |  |
9.方程log2x+x=2的解所在的区间为( )
| A. | (0.5,1) | B. | (1,1.5) | C. | (1.5,2) | D. | (2,2.5) |
6.已知集合A={x∈R|x4+mx-2=0},满足a∈A的所有点M(a,$\frac{2}{a}$)均在直线y=x的同侧,则实数m的取值范围是( )
| A. | (-∞,-$\sqrt{2}$)∪($\sqrt{2}$,+∞) | B. | (-$\sqrt{2}$,-1)∪(1,$\sqrt{2}$) | C. | (-5,-$\sqrt{2}$)∪($\sqrt{2}$,6) | D. | (-∞,-6)∪(6,+∞) |
7.集合A={x|0≤x≤2},B={x|x2-x>0},则A∩B=( )
| A. | R | B. | (-∞,0)∪(1,2) | C. | ∅ | D. | (1,2] |