题目内容
已知△ABC的两个顶点A,B的坐标分别是(0,-1),(0,1),且AC,BC所在直线的斜率之积等于m(m≠0).
(1)求顶点C的轨迹E的方程,并判断轨迹E为何种圆锥曲线;
(2)当m=-
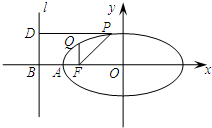
时,过点F(1,0)的直线l交曲线E于M,N两点,设点N关于x轴的对称点为Q(M,Q不重合)试问:直线MQ与x轴的交点是否为定点?若是,求出定点,若不是,请说明理由.
(1)求顶点C的轨迹E的方程,并判断轨迹E为何种圆锥曲线;
(2)当m=-
| 1 |
| 2 |
(1)设点C(x,y),由AC,BC所在直线的斜率之积等于m(m≠0),
得:
•
=m,化简得:-mx2+y2=1(x≠0).
当m<-1时,轨迹E表示焦点在y轴上的椭圆,且除去(0,1),(0,-1)两点;
当m=-1时,轨迹E表示以(0,0)为圆心,半径是1的圆,且除去(0,1),(0,-1)两点;
当-1<m<0时,轨迹E表示焦点在x轴上的椭圆,且除去(0,1),(0,-1)两点;
当m>0时,轨迹E表示焦点在y轴上的双曲线,且除去(0,1),(0,-1)两点.
(2)当m=-
时,曲线E的方程为
+y2=1(x≠0).
由题意可知直线l的斜率存在切不等于0,则可设l:y=k(x-1),
再设M(x1,y1),N(x2,y2),Q(x2,-y2)(x1≠x2).
联立
,得(1+2k2)x2-4k2x+2k2-2=0.
∴x1+x2=
,x1x2=
,
∵M,Q不重合,则x1≠x2,y1≠-y2.
∴MQ所在直线方程为y-y1=
(x-x1),
令y=0,得x=x1+
=x1+
=
=
=2.
∴直线MQ过定点(2,0).
得:
| y-1 |
| x |
| y+1 |
| x |
当m<-1时,轨迹E表示焦点在y轴上的椭圆,且除去(0,1),(0,-1)两点;
当m=-1时,轨迹E表示以(0,0)为圆心,半径是1的圆,且除去(0,1),(0,-1)两点;
当-1<m<0时,轨迹E表示焦点在x轴上的椭圆,且除去(0,1),(0,-1)两点;
当m>0时,轨迹E表示焦点在y轴上的双曲线,且除去(0,1),(0,-1)两点.
(2)当m=-
| 1 |
| 2 |
| x2 |
| 2 |
由题意可知直线l的斜率存在切不等于0,则可设l:y=k(x-1),
再设M(x1,y1),N(x2,y2),Q(x2,-y2)(x1≠x2).
联立
|
∴x1+x2=
| 4k2 |
| 1+2k2 |
| 2k2-2 |
| 1+2k2 |
∵M,Q不重合,则x1≠x2,y1≠-y2.
∴MQ所在直线方程为y-y1=
| y1+y2 |
| x1-x2 |
令y=0,得x=x1+
| y1(x2-x1) |
| y1+y2 |
| k(x1-1)(x2-x1) |
| k(x1+x2-2) |
| 2x1x2-(x1+x2) |
| x1+x2-2 |
=
2•
| ||||
|
∴直线MQ过定点(2,0).

练习册系列答案
相关题目