题目内容
已知圆C经过点A(-2,0),B(0,2),且圆心C在直线y=x上,又直线l:y=kx+1与圆C相交于P、Q两点.
(1)求圆C的方程;
(2)若
.
=-2,求实数k的值.
(1)求圆C的方程;
(2)若
| OP |
| OQ |
(I)设圆C(a,a)半径r.因为圆经过A(-2,0),B(0,2)
所以:|AC|=|BC|=r,解得a=0,r=2,
所以C的方程x2+y2=4.
(II)方法一:
因为,
•
=2×2cos<
,
>=-2,
所以,COS∠POQ=-
,∠POQ=120°,
所以圆心到直l:kx-y+1=0的距离d=1,d=
,所以 k=0.
方法二:P(x1,y1),Q(x2,y2),因
,代入消元(1+k2)x2+2kx-3=0.
由题意得△=4k2-4(1+k2)(-3)>0且x1+x2=
和x1•x2=
因为
•
=x1•x2+y1•y2=-2,
又y1•y2=(kx1+1)(kx2+1)=k2x1x2+k(x1+x2)+1,
所以x1•x2+y1•y2=
+
+
+1=-2,
化简得:-5k2-3+3(k2+1)=0,
所以:k2=0即k=0.
所以:|AC|=|BC|=r,解得a=0,r=2,
所以C的方程x2+y2=4.
(II)方法一:
因为,
| OP |
| OQ |
| OP |
| OQ |
所以,COS∠POQ=-
| 1 |
| 2 |
所以圆心到直l:kx-y+1=0的距离d=1,d=
| 1 | ||
|
方法二:P(x1,y1),Q(x2,y2),因
|
由题意得△=4k2-4(1+k2)(-3)>0且x1+x2=
| -2k |
| 1+k2 |
| -3 |
| 1+k2 |
因为
| OP |
| OQ |
又y1•y2=(kx1+1)(kx2+1)=k2x1x2+k(x1+x2)+1,
所以x1•x2+y1•y2=
| -3 |
| 1+k2 |
| -3k2 |
| 1+k2 |
| -2k2 |
| 1+k2 |
化简得:-5k2-3+3(k2+1)=0,
所以:k2=0即k=0.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
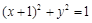 及圆
及圆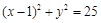 都内切,则动圆圆心C的轨迹方程为 .
都内切,则动圆圆心C的轨迹方程为 .