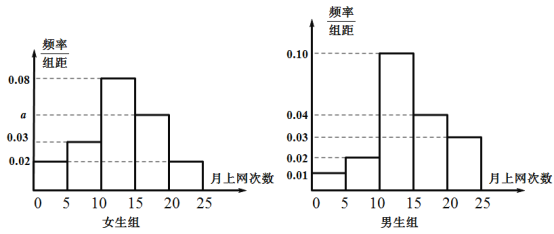
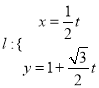题目内容
【题目】某市工会组织了一次工人综合技能比赛,一共有![]() 名工人参加,他们的成绩都分布在
名工人参加,他们的成绩都分布在![]() 内,数据经过汇总整理得到如下的频率分布直方图,规定成绩在
内,数据经过汇总整理得到如下的频率分布直方图,规定成绩在![]() 分及
分及![]() 分以上的为优秀.
分以上的为优秀.

(1)求图中![]() 的值;
的值;
(2)估计这次比赛成绩的平均数(同一组中的数据以这组数据所在区间中点的值作代表);
(3)某工厂车间有![]() 名工人参加这次比赛,他们的成绩分布和整体的成绩分布情况完全一致,若从该车间参赛的且成绩为优秀的工人中任选两人,求这两人成绩均低于
名工人参加这次比赛,他们的成绩分布和整体的成绩分布情况完全一致,若从该车间参赛的且成绩为优秀的工人中任选两人,求这两人成绩均低于![]() 分的概率.
分的概率.
【答案】(1)0.01;(2)69.44;(2)![]() .
.
【解析】
(1)由纵坐标![]() 组距
组距![]() 频率,以及所有组频率之和为
频率,以及所有组频率之和为![]() ,即可列式求出
,即可列式求出![]() ;
;
(2)根据频率分布直方图平均数公式,即可求得结果;
(3)先求出![]() 人中优秀人数为
人中优秀人数为![]() 人,再根据列举法,运用古典概型求出概率;
人,再根据列举法,运用古典概型求出概率;
(1)由频率分布直方图可知:
![]() ,
,
解得:![]()
(2)设这次比赛的平均数为![]() ,则
,则
![]()
![]()
![]()
![]()
(3)![]() 名工人参加比赛,优秀人数为:
名工人参加比赛,优秀人数为:![]() 人,
人,
![]() 名优秀工人中
名优秀工人中![]() 内有
内有![]() 人设为
人设为![]() ,
,![]() 有一人设为
有一人设为![]() ,
,
则![]() 人中选
人中选![]() 人有以下情况:
人有以下情况:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 共有
共有![]() 种情况,
种情况,
![]() 人成绩均低于
人成绩均低于![]() 分有
分有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共6种情况.
,共6种情况.
则![]() 人任选
人任选![]() 人,两人成绩均低于92分的概率无
人,两人成绩均低于92分的概率无![]() .
.

【题目】已知某保险公司的某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | ≥4 |
保费(元) |
|
|
|
|
|
随机调查了该险种的![]() 名续保人在一年内的出险情况,得到下表:
名续保人在一年内的出险情况,得到下表:
出险次数 | 0 | 1 | 2 | 3 | ≥4 |
频数 | 280 | 80 | 24 | 12 | 4 |
该保险公司这种保险的赔付规定如下:
出险序次 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次及以上 |
赔付金额(元) |
|
|
|
|
|
将所抽样本的频率视为概率.
(1)求本年度续保人保费的平均值的估计值;
(2)按保险合同规定,若续保人在本年度内出险![]() 次,则可获得赔付
次,则可获得赔付![]() 元;依此类推,求本年度续保人所获赔付金额的平均值的估计值;
元;依此类推,求本年度续保人所获赔付金额的平均值的估计值;
(3)续保人原定约了保险公司的销售人员在上午![]() 之间上门签合同,因为续保人临时有事,外出的时间在上午
之间上门签合同,因为续保人临时有事,外出的时间在上午![]() 之间,请问续保人在离开前见到销售人员的概率是多少?
之间,请问续保人在离开前见到销售人员的概率是多少?
【题目】低碳经济时代,文化和旅游两大产业逐渐成为我国优先发展的“绿色朝阳产业”.为了解某市的旅游业发展情况,某研究机构对该市2019年游客的消费情况进行随机调查,得到频数分布表及频率分布直方图.
旅游消费(千元) |
|
|
|
|
频数(人) | 10 | 60 |
|
|
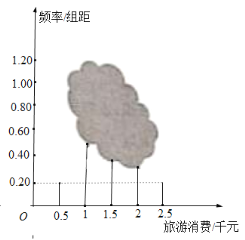
(1)由图表中数据,求![]() 的值及游客人均消费估计值(同一组中的数据以这组数据所在区间中点的值为代表)
的值及游客人均消费估计值(同一组中的数据以这组数据所在区间中点的值为代表)
(2)该机构利用最小二乘法得到2013~2017年该市的年旅游人次![]() (千万人次)与年份代码
(千万人次)与年份代码![]() 的线性回归模型:
的线性回归模型:![]() .
.
注:年份代码1~5分别对应年份2013~2017
①试求2013~2017年的年旅游人次的平均值;
②据统计,2018年该市的年旅游人次为9千万人次.建立2013~2018年该市年旅游人次![]() (千万人次)与年份代码
(千万人次)与年份代码![]() 的线性回归方程,并估计2019年该市的年旅游收入.
的线性回归方程,并估计2019年该市的年旅游收入.
注:年旅游收入=年旅游人次×人均消费
参考数据:![]() .参考公式:
.参考公式: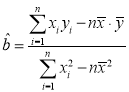 ,
,![]() .
.