题目内容
【题目】大型中华传统文化电视节目《![]() 中国诗词大会》以“赏中华诗词,寻文化基因,品生活之美”为宗旨,深受广大观众喜爱,各基层单位也通过各种形式积极组织、选拔和推荐参赛选手.某单位制定规则如下:(1)凡报名参赛的诗词爱好者必须先后通过笔试和面试,方可获得入围
中国诗词大会》以“赏中华诗词,寻文化基因,品生活之美”为宗旨,深受广大观众喜爱,各基层单位也通过各种形式积极组织、选拔和推荐参赛选手.某单位制定规则如下:(1)凡报名参赛的诗词爱好者必须先后通过笔试和面试,方可获得入围![]() 正赛的推荐资格;(2)笔试成绩不低于85分的选手进入面试,面试成绩最高的3人获得推荐资格.在该单位最近组织的一次选拔活动中,随机抽取了一个笔试成绩的样本,据此绘制成频率分布直方图(如图
正赛的推荐资格;(2)笔试成绩不低于85分的选手进入面试,面试成绩最高的3人获得推荐资格.在该单位最近组织的一次选拔活动中,随机抽取了一个笔试成绩的样本,据此绘制成频率分布直方图(如图![]() .同时,也绘制了所有面试成绩的茎叶图(如图2,单位:分).
.同时,也绘制了所有面试成绩的茎叶图(如图2,单位:分).

(Ⅰ)估计该单位本次报名参赛的诗词爱好者的总人数;
(Ⅱ)若从面试成绩高于(不含)中位数的选手中随机选取3人,设其中获得推荐资格的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
【答案】(Ⅰ)60人;(Ⅱ)分布列见解析,![]()
【解析】
(Ⅰ)由频率分布直方图求出对应的频率,利用茎叶图估计所求的总人数即可;
(Ⅱ)根据题意知,![]() 可能的取值为
可能的取值为![]() ,计算对应概率,列出分布列,代入数学期望公式求解即可.
,计算对应概率,列出分布列,代入数学期望公式求解即可.
(Ⅰ)由频率分布直方图知,笔试成绩不低于85分的频率为![]() ,
,
由茎叶图知,参加面试的人数为15人,
所以估计该单位本次报名参赛的诗词爱好者的总人数为![]() (人
(人![]() ;
;
(Ⅱ)面试成绩高于(不含)中位数的选手有7人,其中获得推荐资格的有3人,
所以从7人中随机选取3人,获得推荐资格的人数![]() ,1,2,3,
,1,2,3,
计算![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
所以随机变量![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以数学期望为![]() .
.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案【题目】大学先修课程是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年,共有![]() 人参与学习先修课程,这两年学习先修课程的学生都参加了高校的自主招生考试(满分
人参与学习先修课程,这两年学习先修课程的学生都参加了高校的自主招生考试(满分![]() 分),结果如下表所示:
分),结果如下表所示:
分数 |
|
|
|
|
|
人数 |
|
|
|
|
|
参加自主招生获得通过的概率 |
|
|
|
|
|
(1)这两年学校共培养出优等生![]() 人,根据图中等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过
人,根据图中等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过![]() 的前提下认为学习先修课程与优等生有关系?
的前提下认为学习先修课程与优等生有关系?
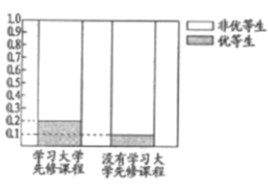
优等生 | 非优等生 | 总计 | |
学习大学先修课程 |
| ||
没有学习大学先修课程 | |||
总计 |
|
(2)已知今年全校有![]() 名学生报名学习大学选项课程,并都参加了高校的自主招生考试,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
名学生报名学习大学选项课程,并都参加了高校的自主招生考试,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
(i)在今年参与大学先修课程学习的学生中任取一人,求他获得高校自主招生通过的概率;
(ii)某班有![]() 名学生参加了大学先修课程的学习,设获得高校自主招生通过的人数为
名学生参加了大学先修课程的学习,设获得高校自主招生通过的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: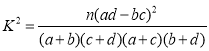 ,其中
,其中![]() .
.