题目内容
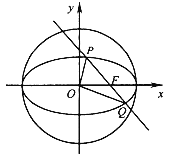
【题目】在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ).
).
(1)写出曲线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若射线![]() (
(![]() )与曲线
)与曲线![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() 两点(不是原点),求
两点(不是原点),求![]() 的最大值.
的最大值.
【答案】(1) 曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ;曲线
;曲线![]() 的普通方程为
的普通方程为![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据极坐标和直角坐标之间的转换公式,以及加减消参的方法,即可求得对应的直角坐标方程和普通方程;
(2)将曲线![]() 的直角方程转化为极坐标方程,联立射线
的直角方程转化为极坐标方程,联立射线![]() ,即可用
,即可用![]() 的三角函数表示出
的三角函数表示出![]() 以及
以及![]() ,再求该三角函数的最大值即可.
,再求该三角函数的最大值即可.
(1)对曲线![]() 的极坐标方程
的极坐标方程![]() 两边同乘以
两边同乘以![]() ,
,
可得![]() ,即可得
,即可得![]() 的直角坐标方程为:
的直角坐标方程为:
![]() ,整理得
,整理得![]() ;
;
曲线![]() 的参数方程为
的参数方程为![]() ,两式相加可得:
,两式相加可得:
![]() ,整理得
,整理得![]() .
.
综上所述:曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ;
;
曲线![]() 的普通方程为
的普通方程为![]() .
.
(2)曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
联立![]() ,即可得
,即可得![]() ,即
,即![]()
又曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,
联立![]() ,即可得
,即可得![]() ,即
,即![]()
故![]()
![]()
![]()
![]()
因为![]() ,故可得
,故可得![]()
则![]() ,
,
即可得![]() 的最大值为
的最大值为![]() .
.
即![]() 的最大值为
的最大值为![]() .
.

【题目】大学先修课程是在高中开设的具有大学水平的课程,旨在让学有余力的高中生早接受大学思维方式、学习方法的训练,为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年,共有![]() 人参与学习先修课程,这两年学习先修课程的学生都参加了高校的自主招生考试(满分
人参与学习先修课程,这两年学习先修课程的学生都参加了高校的自主招生考试(满分![]() 分),结果如下表所示:
分),结果如下表所示:
分数 |
|
|
|
|
|
人数 |
|
|
|
|
|
参加自主招生获得通过的概率 |
|
|
|
|
|
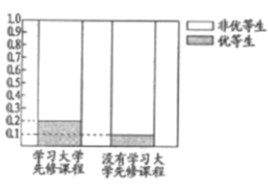
(1)这两年学校共培养出优等生![]() 人,根据图中等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过
人,根据图中等高条形图,填写相应列联表,并根据列联表检验能否在犯错的概率不超过![]() 的前提下认为学习先修课程与优等生有关系?
的前提下认为学习先修课程与优等生有关系?
优等生 | 非优等生 | 总计 | |
学习大学先修课程 |
| ||
没有学习大学先修课程 | |||
总计 |
|
(2)已知今年全校有![]() 名学生报名学习大学选项课程,并都参加了高校的自主招生考试,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
名学生报名学习大学选项课程,并都参加了高校的自主招生考试,以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.
(i)在今年参与大学先修课程学习的学生中任取一人,求他获得高校自主招生通过的概率;
(ii)某班有![]() 名学生参加了大学先修课程的学习,设获得高校自主招生通过的人数为
名学生参加了大学先修课程的学习,设获得高校自主招生通过的人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式: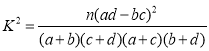 ,其中
,其中![]() .
.