题目内容
已知直线l1经过点A(-3,0),B(3,2),直线l2经过点B,且l1⊥l2.
(Ⅰ)求直线
的方程;
(Ⅱ)设直线l2与直线y=8x的交点为C,求△ABC外接圆的方程.
(Ⅰ)求直线
| l | 2 |
(Ⅱ)设直线l2与直线y=8x的交点为C,求△ABC外接圆的方程.
(Ⅰ)直线l1的斜率为k=
=
,
∵l1⊥l2,∴l2的斜率为k1=
=-3,
又∵直线l2经过点B(3,2),
∴l2的方程为y-2=-3(x-3),即3x+y-11=0;
(Ⅱ)联解直线l2与直线y=8x,得x=1,y=8.
∴直线l2与直线y=8x的交点为C(1,8),
∵
=(6,2),
=(-2,6),
∴
•
=0,可得△ABC是AC为斜边的直角三角形,其外接圆以AC为直径的圆,
求得AC的中点为(-1,4),AC=
=4
,
∴外接圆的圆心为(-1,4),半径R=2
,可得△ABC外接圆的方程为(x+1)2+(y-4)2=20.
| 2-0 |
| 3-(-3) |
| 1 |
| 3 |
∵l1⊥l2,∴l2的斜率为k1=
| -1 |
| k |
又∵直线l2经过点B(3,2),
∴l2的方程为y-2=-3(x-3),即3x+y-11=0;
(Ⅱ)联解直线l2与直线y=8x,得x=1,y=8.
∴直线l2与直线y=8x的交点为C(1,8),
∵
| AB |
| BC |
∴
| AB |
| BC |
求得AC的中点为(-1,4),AC=
| (-3-1)2+(0-8)2 |
| 5 |
∴外接圆的圆心为(-1,4),半径R=2
| 5 |

练习册系列答案
相关题目
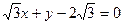 截圆
截圆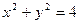 得的劣弧所对的圆心角为( )
得的劣弧所对的圆心角为( )