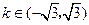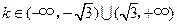题目内容
圆C与直线y=x-2相切于点P，且圆心C在x轴的正半轴上，半径r=
（1）求圆C的方程；
（2）求△POC的面积．（O为坐标原点）
| 2 |
（1）求圆C的方程；
（2）求△POC的面积．（O为坐标原点）
（1）设C（x，0）（x＞0），则
∵圆C与直线y=x-2相切于点P，半径r=
，
∴
=
，
∵x＞0，
∴x=4，
∴圆C的方程为（x-4）2+y2=2；
（2）过C且与直线y=x-2垂直的直线方程为y=-x+4，与直线y=x-2，
联立可得x=3，y=1，即P（3，1），
∴△POC的面积为
•(4-0)•1=2．
∵圆C与直线y=x-2相切于点P，半径r=
| 2 |
∴
| |x-2| | ||
|
| 2 |
∵x＞0，
∴x=4，
∴圆C的方程为（x-4）2+y2=2；
（2）过C且与直线y=x-2垂直的直线方程为y=-x+4，与直线y=x-2，
联立可得x=3，y=1，即P（3，1），
∴△POC的面积为
| 1 |
| 2 |
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
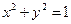与直线
没有公共点的充要条件是（ ）
