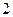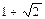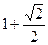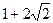题目内容
三角形ABC,顶点A(1,0),B(2,2
),C(3,0),该三角形的内切圆方程为( )
| 2 |
A.(x-2)2+(y+
| B.(x-2)2+(y-
| ||||||||||||
C.(x-
| D.(x-2)2+(y-
|
∵A(1,0),B(2,2
),C(3,0),
∴可得|AB|=3,|AC|=2,|BC|=3
三角形的面积S=
|AC|•yB=2
,周长为3+2+3=8
因此,三角形的内切圆半径r=
=
又∵圆心为∠BAC平分线与∠BCA平分线的交点
∴算出圆心坐标为(2,
),
可得该三角形的内切圆方程为(x-2)2+(y-
)2=
故选:D
| 2 |
∴可得|AB|=3,|AC|=2,|BC|=3
三角形的面积S=
| 1 |
| 2 |
| 2 |
因此,三角形的内切圆半径r=
| 2S |
| |AB|+|AC|+|BC| |
| ||
| 2 |
又∵圆心为∠BAC平分线与∠BCA平分线的交点
∴算出圆心坐标为(2,
| ||
| 2 |
可得该三角形的内切圆方程为(x-2)2+(y-
| ||
| 2 |
| 1 |
| 2 |
故选:D

练习册系列答案
相关题目
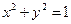 与直线
与直线 没有公共点的充要条件是( )
没有公共点的充要条件是( )

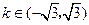
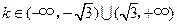
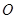 引圆
引圆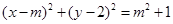 的切线
的切线 ,当
,当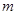 变化时,切点
变化时,切点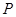 的轨迹方程是( )
的轨迹方程是( )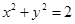

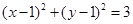
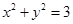
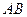 是圆O的直径,
是圆O的直径, 切圆O于
切圆O于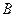 点,
点, 切圆O于
切圆O于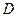 点,交
点,交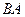 的延长线于
的延长线于 点,若
点,若 ,
,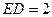 ,则
,则 _________。
_________。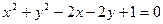 上的点到直线
上的点到直线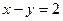 的距离最大值是( )
的距离最大值是( )