Question

在棱长为2的正方体ABCD-A₁B₁C₁D₁中，E，F分别为A₁B₁，CD的中点．
（1）求直线EC与AF所成角的余弦值；
（2）求二面角E-AF-B的余弦值．

Answer 1

（1）建立空间直角坐标系．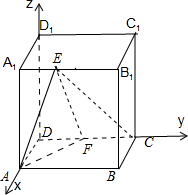
则A（2，0，0），F（0，1，0），C（0，2，0），E（2，1，2），
∴

AF

=(-2，1，0)，

CE

=(2，-1，2)．
∴cos＜

AF，

CE

＞=

-4-1

(-2)2+12 • 22+(-1)2+22

=-

5

3

，
故直线EC与AF所成角的余弦值为

5

3

．
（2）平面ABCD的一个法向量为

n1

=(0，0，1)．
设平面AEF的一个法向量为

n2

=(x，y，z)，
∵

AF

=(-2，1，0)，

AE

=(0，1，2)，∴

-2x+y=0 y+2z=0

，
令x=1，则y=2，z=-1⇒

n2

=(1，2，-1)，
∴cosθ=|

n1 • n2

| n1 || n2 |

|=|

-1

1+4+1

|=

6

6

．
由图知二面角E-AF-B为锐二面角，其余弦值为

6

6

．