题目内容
14.三棱柱ABC-A1B1C1的底是边长为1的正三角形,高AA1=1,在AB上取一点P,设△PA1C1与面A1B1C1所成的二面角为α,△PB1C1与面A1B1C1所成的二面角为β,则tan(α+β)的最小值是-$\frac{8\sqrt{3}}{13}$.分析 作PP1⊥A1B1,过P1作P1H⊥A1C1,由三垂线定理得∠PHP1=α,设AP=x,求出tanα,同理求出tanβ,由此利用正切加法定理能求出tan(α+β)的最小值.
解答 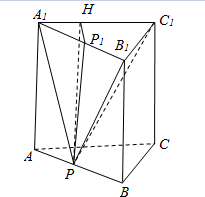 解:作PP1⊥A1B1,则PP1是三棱柱的高.
解:作PP1⊥A1B1,则PP1是三棱柱的高.
过P1作P1H⊥A1C1,连结PH,则∠PHP1=α,
设AP=x,BP=1-x(0≤x≤1),则$tanα=\frac{2}{{\sqrt{3}x}}$,
同理$tanβ=\frac{2}{{\sqrt{3}(1-x)}}$,
∴$tan(α+β)=\frac{{2\sqrt{3}}}{3x(1-x)-4}≥-\frac{8}{13}\sqrt{3}$(当$x=\frac{1}{2}$时取等号),
∴tan(α+β)的最小值是-$\frac{8\sqrt{3}}{13}$.
故答案为:-$\frac{8\sqrt{3}}{13}$.
点评 本题考查两角和正切的最小值的求法,是中档题,解题时要认真审题,注意三垂线定理和正切加法定理的合理运用.

练习册系列答案
相关题目
4.已知m为一条直线,α,β为两个不同的平面,则下列说法正确的是( )
| A. | 若m∥α,α∥β,则m∥β | B. | 若α⊥β,m⊥α,则m⊥β | C. | 若m∥α,α⊥β,则m⊥β | D. | 若m⊥α,α∥β,则m⊥β |
19.方程lnx+2x=6的解一定位于区间( )
| A. | .(1,2) | B. | (2,3) | C. | .(3,4) | D. | (4,5) |
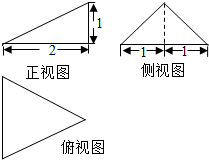 某三棱锥的三视图如图所示,则该三棱锥的4个面中,直角三角形的个数是1个,它的表面积是21.
某三棱锥的三视图如图所示,则该三棱锥的4个面中,直角三角形的个数是1个,它的表面积是21.