题目内容
2.已知函数$f(x)=cos({2x-\frac{π}{3}})+{sin^2}x-{cos^2}x+\sqrt{2}$.(1)求函数f(x)的最小正周期和单调递增区间;
(2)若存在$t∈[{\frac{π}{12},\frac{π}{3}}]$满足[f(t)]2-2$\sqrt{2}$f(t)-m>0,求实数m的取值范围.
分析 (1)利用三角函数恒等变换的应用化简函数解析式可得f(x)=sin(2x-$\frac{π}{6}$)+$\sqrt{2}$,由周期公式可求函数f(x)的最小正周期,由$2kπ-\frac{π}{2}≤2x-\frac{π}{6}≤2kπ+\frac{π}{2}$(k∈Z),即可解得单调递增区间.
(2)当$t∈[{\frac{π}{12},\frac{π}{3}}]$时,可得:$2t-\frac{π}{6}∈[{0,\frac{π}{2}}]$,解得:$f(t)=sin({2t-\frac{π}{6}})+\sqrt{2}∈[{\sqrt{2},\sqrt{2}+1}]$,利用二次函数的性质即可得解.
解答 解:(1)∵$f(x)=\frac{1}{2}cos2x+\frac{{\sqrt{3}}}{2}sin2x+{sin^2}x-{cos^2}x+\sqrt{2}$
=$\frac{1}{2}cos2x+\frac{{\sqrt{3}}}{2}sin2x-cos2x+\sqrt{2}=sin({2x-\frac{π}{6}})+\sqrt{2}$,
∴函数f(x)的最小正周期T=π.
∵由$2kπ-\frac{π}{2}≤2x-\frac{π}{6}≤2kπ+\frac{π}{2}$(k∈Z),得$kπ-\frac{π}{6}≤x≤kπ+\frac{π}{3}$(k∈Z),
∴单调递增区间为$[{kπ-\frac{π}{6},kπ+\frac{π}{3}}]$(k∈Z).
(2)当$t∈[{\frac{π}{12},\frac{π}{3}}]$时,可得:$2t-\frac{π}{6}∈[{0,\frac{π}{2}}]$,
解得:$f(t)=sin({2t-\frac{π}{6}})+\sqrt{2}∈[{\sqrt{2},\sqrt{2}+1}]$
$⇒F(t)={[f(t)]^2}-2\sqrt{2}f(t)={[f(t)-\sqrt{2}]^2}-2∈[{-2,-1}]$.
存在$t∈[{\frac{π}{12},\frac{π}{3}}]$,满足F(t)-m>0的实数m的取值范围为(-∞,-1).
点评 本题主要考查了三角函数恒等变换的应用,正弦函数的图象和性质,考查了二次函数的图象和性质,属于基本知识的考查.

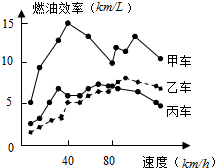 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )| A. | 甲车 | B. | 乙车 | C. | 丙车 | D. | 无法确定 |
| A. | {1} | B. | {-1} | C. | {1,-1} | D. | {-1,0,1} |
| A. | $\frac{{{a^2}+{b^2}}}{2}≥{(\frac{a+b}{2})^2}$ | B. | $\frac{b}{a}+\frac{a}{b}≥2$ | C. | $(a+b)(\frac{1}{a}+\frac{1}{b})≥4$ | D. | $\frac{|a+b|}{2}≥\sqrt{\;|ab|}$ |
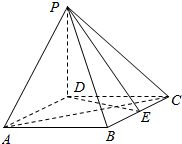 如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥底面ABCD,AD=2,∠DAB=60°,E为BC的中点.
如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥底面ABCD,AD=2,∠DAB=60°,E为BC的中点.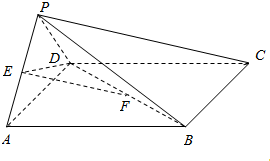 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,侧面PAD⊥底面ABCD,E,F分别为PA,BD的中点,PA=PD=AD=2,$AB=2\sqrt{2}$,∠DAB=45°.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,侧面PAD⊥底面ABCD,E,F分别为PA,BD的中点,PA=PD=AD=2,$AB=2\sqrt{2}$,∠DAB=45°.