题目内容
5.若命题“?a∈[2,4],使ax2+(a-3)x-3>0”是真命题,则实数x的取值范围是$(-∞,-1)∪(\frac{3}{4},+∞)$.分析 令f(a)=(x2+x)a-3x-3,由题意得f(2)>0 或f(4)>0,由此求出实数x的取值范围.
解答 解:令f(a)=ax2+(a-3)x-3=(x2+x)a-3x-3,是关于a的一次函数,
由题意得:
2(x2+x)-3x-3>0,或 4(x2+x)-3x-3>0.
即2x2 -x-3>0或4x2+x-3>0.
取并得x<-1或x>$\frac{3}{4}$.
故答案为:(-∞,-1)∪($\frac{3}{4}$,+∞).
点评 本题是一个存在性问题,由题设条件转化得到2(x2+x)-3x-3>0,或 4(x2+x)-3x-3>0,是解题的关键.

练习册系列答案
相关题目
13.设f:x→x2是集合A到B的函数,如果集合B={1},则集合A不可能是( )
| A. | {1} | B. | {-1} | C. | {1,-1} | D. | {-1,0,1} |
17.若a和b均为非零实数,则下列不等式中恒成立的是 ( )
| A. | $\frac{{{a^2}+{b^2}}}{2}≥{(\frac{a+b}{2})^2}$ | B. | $\frac{b}{a}+\frac{a}{b}≥2$ | C. | $(a+b)(\frac{1}{a}+\frac{1}{b})≥4$ | D. | $\frac{|a+b|}{2}≥\sqrt{\;|ab|}$ |
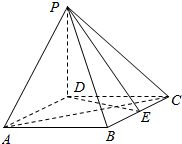 如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥底面ABCD,AD=2,∠DAB=60°,E为BC的中点.
如图,四棱锥P-ABCD的底面ABCD为菱形,PD⊥底面ABCD,AD=2,∠DAB=60°,E为BC的中点.