题目内容
4.已知m为一条直线,α,β为两个不同的平面,则下列说法正确的是( )| A. | 若m∥α,α∥β,则m∥β | B. | 若α⊥β,m⊥α,则m⊥β | C. | 若m∥α,α⊥β,则m⊥β | D. | 若m⊥α,α∥β,则m⊥β |
分析 对四个选项,分别进行判断,即可得出结论.
解答 解:对于A,若m∥α,α∥β,则m∥β或m?β,不正确;
对于B,∵α⊥β,∴设α∩β=a,在平面β内作直线b⊥a,则b⊥α,∵m⊥α,∴m∥b,
若m?β,则m∥β,若m?β,也成立.∴m∥β或m?β,不正确;
对于C,若m∥α,α⊥β,则则m∥β或m,β相交,不正确;
对于D,若m⊥α,α∥β,利用平面与平面平行的性质,可得m⊥β,正确.
故选:D.
点评 本题主要考查了直线,平面之间的位置关系的判断,需要学生具备空间想象力,逻辑推理能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.若双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上存在一点P满足|OP|为边长的正方形的面积等于2ab(其中O为坐标原点),则双曲线的离心率的取值范围是( )
| A. | (1,$\frac{\sqrt{5}}{2}$] | B. | (1,$\frac{\sqrt{7}}{2}$] | C. | [$\frac{\sqrt{5}}{2}$,+∞) | D. | [$\frac{\sqrt{7}}{2}$,+∞) |
12.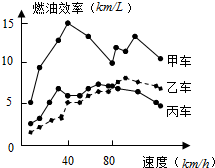 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )
 汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )
汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,如图描述了甲、乙、丙三两汽车在不同速度下的燃油效率情况.某城市机动车最高限速80千米/小时,相同条件下,用甲、乙、丙三两汽车在该市行驶,最省油是( )| A. | 甲车 | B. | 乙车 | C. | 丙车 | D. | 无法确定 |
9.设集合A={x丨-2≤x<4},B={x丨x2-ax-4≤0},若B⊆A,则实数a的取值范围为( )
| A. | [-1,2] | B. | [-1,2) | C. | [0,3) | D. | [0,3] |
13.设f:x→x2是集合A到B的函数,如果集合B={1},则集合A不可能是( )
| A. | {1} | B. | {-1} | C. | {1,-1} | D. | {-1,0,1} |