题目内容
【题目】设函数
，
．
（1）若函数f（x）在
处有极值，求函数f（x）的最大值；
（2）是否存在实数b，使得关于x的不等式
在
上恒成立？若存在，求出b的取值范围；若不存在，说明理由；
【答案】（1）函数f（x）的最大值为
（2）存在
，详见解析
【解析】
（1）函数f（x）在
处有极值说明
（2）对
求导，并判断其单调性。
解：（1）由已知得：
，且函数f（x）在处有极值
∴
，
∴
∴
，
∴
当
时，
，f（x）单调递增；
当
时，
，f（x）单调递减；
∴函数f（x）的最大值为
．
（2）由已知得：
①若
，则
时，
∴
在
上为减函数，
∴
在
上恒成立；
②若
，则时，
∴在[0，+∞）上为增函数，
∴
，
不能使
在上恒成立；
③若
，则
时，
，
当
时，
，
∴在
上为增函数，
此时，
∴不能使在上恒成立；
综上所述，b的取值范围是．
练习册系列答案
相关题目
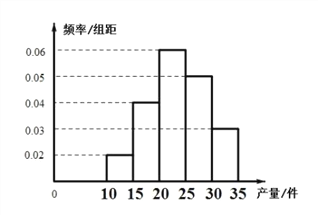
【题目】在倡导低碳、节能减排政策的推动下，越来越多的消费者选择购买新能源汽车.某品牌新能源汽车的行驶里程x（万公里）与该里程内维修保养的总费用y（千元）的统计数据如下：
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0.8 | 1.8 | 3.3 | 4.5 | 4.7 | 6.8 |
（1）根据表中数据建立y关于x的回归方程为
.我们认为，若残差绝对值
，则该数据为可疑数据，请找出上表中的可疑数据；
（2）经过确认，数据采集有误，（1）中可疑数据的维修保养总费用应增加0.7千元.请重新利用线性回归模型拟合数据.（精确到0.01）
附：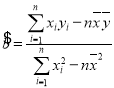
，
.
，
，
，
.
