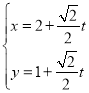题目内容
【题目】已知两点A(﹣2,0)、B(2,0),动点P满足![]() .
.
(1)求动点P的轨迹Ω的方程;
(2)若椭圆![]() 上点(x0,y0)处的切线方程是
上点(x0,y0)处的切线方程是![]() :
:
①过直线l:x=4上一点M引Ω的两条切线,切点分别是P、Q,求证:直线PQ恒过定点N;
②是否存在实数λ,使得|PN|+|QN|=λ|PN||QN|?若存在,求出λ的值;若不存在,说明理由.
【答案】(1)![]() (y≠0);(2)①见解析②存在,
(y≠0);(2)①见解析②存在,![]()
【解析】
(1)设![]() ,再根据斜率之积列式求解即可.
,再根据斜率之积列式求解即可.
(2)①根据题中所给的切线方程,设![]() ,进而求得过
,进而求得过![]() 的切线方程,再代入
的切线方程,再代入![]() 坐标即可求得
坐标即可求得![]() 的直线方程,再分析定点即可.
的直线方程,再分析定点即可.
②由①有![]() ,代入椭圆方程求得交点
,代入椭圆方程求得交点![]() 关于纵坐标的韦达定理,进而表达出
关于纵坐标的韦达定理,进而表达出![]() 的关系式,再化简求解即可.
的关系式,再化简求解即可.
(1)设P(x,y),由题意kPAkPB![]() ,整理得:
,整理得:![]() (y≠0),
(y≠0),
所以动点P的轨迹Ω的方程:![]() (y≠0);
(y≠0);
(2)①设切点P(x1,y1),Q(x2,y2),由题意设M(4,t),则切线方程分别是:![]() ,
,![]() 1,
1,
因为两条切线过M点,则x1![]() 1,x2
1,x2![]() 1,
1,
即P,Q的坐标满足方程:x![]() y=1,而两点确定唯一的直线,
y=1,而两点确定唯一的直线,
所以直线PQ的方程:x![]() y=1,
y=1,
显然对任意的t值,点(1,0)都适合,
所以直线PQ恒过定点N(1,0);
②将直线PQ方程:x![]() y+1代入椭圆中整理得:3(
y+1代入椭圆中整理得:3(![]() 1)2+4y2﹣12=0,
1)2+4y2﹣12=0,
即(12+t2)y2﹣6ty﹣27=0
∴y1+y2![]() ,y1y2
,y1y2![]() ,设y1>0,y2<0,
,设y1>0,y2<0,
因为|PN|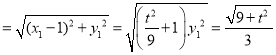 y1,
y1,
同理|QN|![]() ,
,
所以![]()
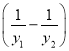
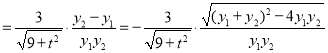
![]()
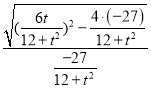
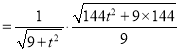
![]() .
.
即|PN|+|QN|![]() |PN||QN|
|PN||QN|
故存在实数![]() ,使得|PN|+|QN|=λ|PN||QN|恒成立.
,使得|PN|+|QN|=λ|PN||QN|恒成立.

【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据
(吨)标准煤的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: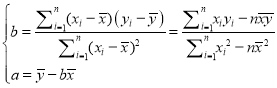
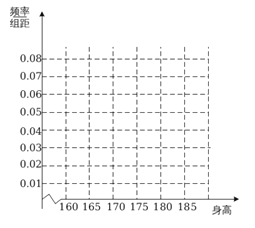
【题目】某中学从高三男生中随机抽取n名学生的身高,将数据整理,得到的频率分布表如表所示:
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.05 |
第2组 |
| a | 0.35 |
第3组 |
| 30 | b |
第4组 |
| 20 | 0.20 |
第5组 |
| 10 | 0.10 |
合计 | n | 1.00 | |
(1)求出频率分布表中![]() 的值,并完成下列频率分布直方图;
的值,并完成下列频率分布直方图;
(2)为了能对学生的体能做进一步了解,该校决定在第1,4,5组中用分层抽样取7名学生进行不同项目的体能测试,若在这7名学生中随机抽取2名学生进行引体向上测试,求第4组中至少有一名学生被抽中的概率.