题目内容
【题目】已知数列{an}的前n项和为Sn , 且Sn=n﹣5an﹣85,n∈N+ .
(1)求an .
(2)求数列{Sn}的通项公式,并求出n为何值时,Sn取得最小值?并说明理由.(参考数据:lg 2≈0.3,lg 3≈0.48).
【答案】
(1)解:∵Sn=n﹣5an﹣85,∴当n=1时,S1=1﹣5a1﹣85,
即a1=1﹣5a1﹣85,解得a1=﹣14;
当n≥2时,an=Sn﹣Sn﹣1=(n﹣5an﹣85)﹣[(n﹣1)﹣5an﹣1﹣85]=﹣5an+5an﹣1+1,
整理得6an=5an﹣1+1,∴6(an﹣1)=5(an﹣1﹣1),
∴ ![]() =
= ![]() .又a1﹣1=﹣15,
.又a1﹣1=﹣15,
∴数列{an﹣1}是以﹣15为首项, ![]() 为公比的等比数列.
为公比的等比数列.
∴an=﹣15×( ![]() )n﹣1+1
)n﹣1+1
(2)解:由(1)知,an=﹣15×( ![]() )n﹣1+1,
)n﹣1+1,
代入Sn=n﹣5an﹣85得,Sn=n﹣5[﹣15×( ![]() )n﹣1+1]﹣85
)n﹣1+1]﹣85
=n+75×( ![]() )n﹣1﹣90.
)n﹣1﹣90.
设Sk为最小值,则 ![]() ,即有
,即有 ![]() ,
,
即 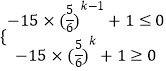 ,即
,即 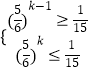 ,可得
,可得 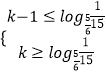 ,
,
即 ![]() ≤k≤
≤k≤ ![]() +1,又
+1,又 ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
lg2≈0.3,lg3≈0.48,∴ ![]() ≈14.75.
≈14.75.
∴14.75≤k≤15.75.又∵k∈N+,∴k=15.
即当n=15时,Sn取得最小值
【解析】(1)运用数列的通项与求和的关系:当n=1时,a1=S1 , 当n≥2时,an=Sn﹣Sn﹣1 , 通过构造数列,结合等比数列的定义和通项公式,即可得到所求;(2)将(1)的结论代入条件,可得Sn=n+75×( ![]() )n﹣1﹣90.设Sk为最小值,则
)n﹣1﹣90.设Sk为最小值,则 ![]() ,运用通项公式,结合对数函数的单调性,解不等式计算即可得到所求k的值.
,运用通项公式,结合对数函数的单调性,解不等式计算即可得到所求k的值.
【考点精析】本题主要考查了数列的前n项和和数列的通项公式的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系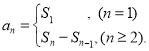 ;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.
;如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】![]() 是指大气中直径小于或等于
是指大气中直径小于或等于![]() 微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大.我国
微米的颗粒物,也称为可入肺颗粒物,对人体健康和大气环境质量的影响很大.我国![]() 标准采用世卫组织设定的最宽限值.即
标准采用世卫组织设定的最宽限值.即![]() 日均值在35微克/立方米以下空气质量为一级;在35微克/立方米
日均值在35微克/立方米以下空气质量为一级;在35微克/立方米![]() 75微克/立方米之间空气质量为二级;75微克/立方米以上空气质量为超标.
75微克/立方米之间空气质量为二级;75微克/立方米以上空气质量为超标.
某市环保局从360天的市区![]() 监测数据中统计了1月至10月的每月的平均值(单位:微克/立方米),如下表所示.
监测数据中统计了1月至10月的每月的平均值(单位:微克/立方米),如下表所示.
月份 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 32 | 28 | 25 | 31 | 34 | 33 | 45 | 44 | 63 | 68 |
(1)从5月到10月的这6个数据中任取2个数值,求这个2个数值均为二级的概率;
(2)求月均值![]() 关于月份
关于月份![]() 的回归直线方程
的回归直线方程![]() ,其中
,其中![]() .
.