题目内容
【题目】一个几何体的三视图如图所示(单位长度为:cm): 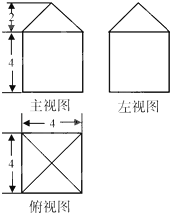
(1)求该几何体的体积;
(2)求该几何体的表面积.
【答案】
(1)解:由三视图知:几何体是正四棱锥与正方体的组合体,
其中正方体的棱长为4,正四棱锥的高为2,
∴几何体的体积V=43+ ![]() ×42×2=
×42×2= ![]()
(2)解:正四棱锥侧面上的斜高为2 ![]() ,
,
∴几何体的表面积S=5×42+4× ![]() ×4×2
×4×2 ![]() =
= ![]()
【解析】(1)几何体是正四棱锥与正方体的组合体,根据三视图判断正方体的棱长及正四棱锥的高,代入棱锥与正方体的体积公式计算;(2)利用勾股定理求出正四棱锥侧面上的斜高,代入棱锥的侧面积公式与正方体的表面积公式计算.
【考点精析】利用由三视图求面积、体积对题目进行判断即可得到答案,需要熟知求体积的关键是求出底面积和高;求全面积的关键是求出各个侧面的面积.

练习册系列答案
相关题目

