题目内容
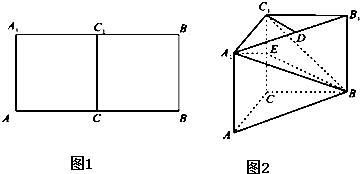
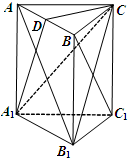
在长方形AA1B1B中,AB=2AA1,C,C1分别AB,A1B1是的中点(如图1).将此长方形沿CC1对折,使平面AA1C1C⊥平面CC1B1B(如图2),已知D,E分别是A1B1,CC1的中点.
(1)求证:C1D∥平面A1BE;
(2)求证:平面A1BE⊥平面AA1B1B.
(1)求证:C1D∥平面A1BE;
(2)求证:平面A1BE⊥平面AA1B1B.

(1)取A1B的中点F,连结DF,EF,
∵D,F分别为A1B1,A1B的中点,∴DF是△A1BB1的中位线,
即四边形C1EFD为平行四边形,
∴EF∥C1D
∵EF?平面A1BE,
∴C1D∥平面A1BE.…(4分)
(2)依题意:平面A1B1C1⊥平面A1BBA,
∵D为A1B1的中点,且三角形A1C1B1为等腰直角三角形,
∴C1D⊥A1B1,由面面垂直的性质定理得C1D⊥平面A1BB1A,…(6分)
又∵C1D∥EF,∴EF⊥平面A1BB1A,
∵EF?平面A1BE,
平面A1BE⊥平面AA1B1B.…(8分)

∵D,F分别为A1B1,A1B的中点,∴DF是△A1BB1的中位线,
|
即四边形C1EFD为平行四边形,
∴EF∥C1D
∵EF?平面A1BE,
∴C1D∥平面A1BE.…(4分)
(2)依题意:平面A1B1C1⊥平面A1BBA,
∵D为A1B1的中点,且三角形A1C1B1为等腰直角三角形,
∴C1D⊥A1B1,由面面垂直的性质定理得C1D⊥平面A1BB1A,…(6分)
又∵C1D∥EF,∴EF⊥平面A1BB1A,
∵EF?平面A1BE,
平面A1BE⊥平面AA1B1B.…(8分)


练习册系列答案
相关题目
 底面ABCD,PA=AD=DC=
底面ABCD,PA=AD=DC=