题目内容
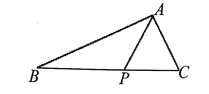
【题目】如图，在四面体
中，已知
⊥平面
， 
， 
， 
为
的中点．
（1）求证： 
；
（2）若
为
的中点，点
在直线
上，且
，
求证：直线
//平面
．
【答案】(1)见解析（2）见解析.
【解析】试题分析：（1）由等腰三角形性质得AD⊥PC．再根据PA⊥平面ABC，得PA⊥BC．最后根据线面垂直判定定理得BC⊥平面PAC，得BC ⊥AD．即得AD⊥平面PBC，可得AD⊥BD（2）设BD与CM交于点G，先根据平几知识得AD//NG，再根据线面平行判定定理得结论
试题解析：(1) ∵PA=AC，D为PC的中点，∴AD⊥PC．
∵ PA⊥平面ABC，BC
平面ABC， ∴ PA⊥BC．
∵ ∠ACB=90°，BC ⊥AC，且PA
AC =A， 
平面
∴ BC⊥平面PAC．
∵ AD
平面PAC， ∴ BC ⊥AD．
且
平面
，
∴AD⊥平面PBC ．
∵ BD
平面PBC，∴AD⊥BD ．
（2） 连接DM，设BD与CM交于点G，连接N G，
∵ D、M为中点，∴DM //BC且
，
∴ DG:GB=DM:BC=1:2．
∵ AN:NB=1:2，∴AN:NB= DG:GB ．
∴ △BNG∽△BAD，∴AD//NG，
∵
平面CMN， 
平面CMN，
∴ 直线AD//平面CMN．
点睛:垂直、平行关系证明中应用转化与化归思想的常见类型.
(1)证明线面、面面平行，需转化为证明线线平行.
(2)证明线面垂直，需转化为证明线线垂直.
(3)证明线线垂直，需转化为证明线面垂直.
练习册系列答案
相关题目
