某几何体的三视图如图所示.该几何体的表面积为( )A．12+$\sqrt{3}+\sqrt{7}$B．4+3$\sqrt{3}+\sqrt{7}$C．8+$\sqrt{3}+\sqrt{7}$D．4+$\sqrt{3}+\sqrt{7}$ 题目和参考答案——青夏教育精英家教网—

题目内容

14．某几何体的三视图如图所示，该几何体的表面积为（　　）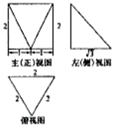

A．

12+$\sqrt{3}+\sqrt{7}$

B．

4+3$\sqrt{3}+\sqrt{7}$

C．

8+$\sqrt{3}+\sqrt{7}$

D．

4+$\sqrt{3}+\sqrt{7}$

分析由已知中的三视图可得：该几何体是一个以正视图为底面的四棱锥，分别计算各个面的面积，可得答案．

解答解：由已知中的三视图可得：该几何体是一个以正视图为底面的四棱锥，
其直观图如下所示：

底面BCDE的面积为：4，
侧面△ABC的面积为$\sqrt{3}$，
侧面△ABE和△ACD的面积均为2，
侧面△ADE的面积为$\sqrt{7}$，
故该几何体的表面积为8+$\sqrt{3}+\sqrt{7}$，
故选：C．

点评本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．

练习册系列答案

5．已知函数f（x）=e^x-$\frac{1}{2}{x^2}$-ax（a∈R）．
（Ⅰ）若函数f（x）的图象在x=0处的切线方程为y=2x+b，求a，b的值；
（Ⅱ）若函数f（x）≥1在$[\frac{1}{2}，+∞）$上恒成立，求实数a的取值范围；
（Ⅲ）如果函数$g（x）=f（x）-（a-\frac{1}{2}）{x^2}$恰有两个不同的极值点x₁，x₂，证明：$\frac{{{x_1}+{x_2}}}{2}$＜ln（2a）．

2．已知非零向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足|$\overrightarrow{a}$|≥1，|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|=2，（$\overrightarrow{c}$-$\overrightarrow{a}$）•（$\overrightarrow{c}$-$\overrightarrow{b}$）=3，则|$\overrightarrow{b}$|的最大值是$\sqrt{3}$；|$\overrightarrow{c}$|的取值范围是[1，3]．

9．

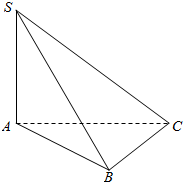如图所示，在三棱锥S-ABC中，△ABC是等腰三角形，AB=BC=2a，∠ABC=120°，SA=2a，且SA⊥平面ABC，则点A到平面SBC的距离为（　　）

A．

$\frac{3a}{2}$

B．

$\frac{2\sqrt{21}}{7}$a

19．长方体各面所在平面将空间分成27部分．

6．下列说法错误的是（　　）

	A．	若棱柱的底面边长相等，则它的各个侧面的面积相等
	B．	九棱柱有9条侧棱，9个侧面，侧面为平行四边形
	C．	六角螺帽、三棱镜的外形都是棱柱
	D．	正四棱台的侧面不一定是等腰梯形

3．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0），设$\frac{x}{a}$+$\frac{y}{b}$=t，若以t为参数，求出双曲线的参数方程．

4．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的实轴长为6，抛物线y²=20x的准线经过双曲线左焦点，过原点的直线与双曲线左、右两支分别交于A，B两点，P为双曲线上不同于A，B的任一点，当k_PA，k_PB存在时，k_PA•k_PB的值为（　　）

试题分类