题目内容
4.若函数y=sin($\frac{π}{3}$-2x),则函数在[-π,0]上的单调递减区间是[-$\frac{π}{12}$,0]和,[-π,-$\frac{7π}{12}$].分析 先求出函数在R上的单调减区间,再判断在[-π,0]上的单调递减区间.
解答 解:∵y=sin($\frac{π}{3}$-2x)=-sin(2x-$\frac{π}{3}$),
∴由2kπ$-\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ$+\frac{π}{2}$,k∈z,
即kπ-$\frac{π}{12}$≤x≤kπ+$\frac{5π}{12}$,k∈z,
当k=0时,-$\frac{π}{12}$≤x≤$\frac{5π}{12}$,
当k=-1时,-$\frac{13π}{12}$≤x≤-$\frac{7π}{12}$,
∵x∈[-π,0],
∴函数在[-π,0]上的单调递减区间为[-$\frac{π}{12}$,0]和,[-π,-$\frac{7π}{12}$],
故答案为:[-$\frac{π}{12}$,0]和,[-π,-$\frac{7π}{12}$]
点评 本题考查了三角形函数的单调区间的求解,结合三角函数的单调性是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14. 如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )
如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )
 如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )
如图,过双曲线的右焦点F分别作两条渐近线的垂线,垂足为M、N,若$\overrightarrow{FM}$•$\overrightarrow{FN}$<0,则此双曲线离心率的取值范围是( )| A. | (1,$\sqrt{2}$) | B. | (1,2) | C. | ($\sqrt{2}$,+∞) | D. | (2,+∞) |
13.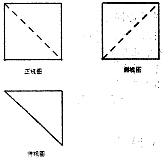 如图是某几何体的三视图,其中正视图、左视图均为正方形,俯视图是腰长为2的等腰三角腰形,则该几何体的体积是( )
如图是某几何体的三视图,其中正视图、左视图均为正方形,俯视图是腰长为2的等腰三角腰形,则该几何体的体积是( )
 如图是某几何体的三视图,其中正视图、左视图均为正方形,俯视图是腰长为2的等腰三角腰形,则该几何体的体积是( )
如图是某几何体的三视图,其中正视图、左视图均为正方形,俯视图是腰长为2的等腰三角腰形,则该几何体的体积是( )| A. | $\frac{8}{3}$ | B. | $\frac{8}{3}$$\sqrt{2}$ | C. | $\frac{4}{3}$ | D. | 4 |
14.某几何体的三视图如图所示,该几何体的表面积为( )
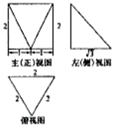

| A. | 12+$\sqrt{3}+\sqrt{7}$ | B. | 4+3$\sqrt{3}+\sqrt{7}$ | C. | 8+$\sqrt{3}+\sqrt{7}$ | D. | 4+$\sqrt{3}+\sqrt{7}$ |
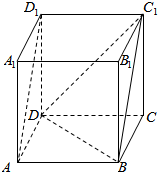 如图,在正方形ABCD-A1B1C1D1中,
如图,在正方形ABCD-A1B1C1D1中, 如图,四边形ABCD是矩形,四边形BCEF是直角梯形,平面ABCD⊥平面BCEF,∠FBC是直角,AB=1,BC=BF=2,CE=4,P、Q、R分别是AF、DF、DE的中点.
如图,四边形ABCD是矩形,四边形BCEF是直角梯形,平面ABCD⊥平面BCEF,∠FBC是直角,AB=1,BC=BF=2,CE=4,P、Q、R分别是AF、DF、DE的中点.