题目内容
2.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$满足|$\overrightarrow{a}$|≥1,|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,($\overrightarrow{c}$-$\overrightarrow{a}$)•($\overrightarrow{c}$-$\overrightarrow{b}$)=3,则|$\overrightarrow{b}$|的最大值是$\sqrt{3}$;|$\overrightarrow{c}$|的取值范围是[1,3].分析 由|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,可得$\overrightarrow{a}⊥\overrightarrow{b}$,可设$\overrightarrow{a}$=(m,0),$\overrightarrow{b}$=(0,n),由条件可得m2+n2=4,结合|$\overrightarrow{a}$|≥1,得|$\overrightarrow{b}$|$≤\sqrt{3}$;设$\overrightarrow{c}$=(x,y),由条件($\overrightarrow{c}$-$\overrightarrow{a}$)•($\overrightarrow{c}$-$\overrightarrow{b}$)=3,可得(x-m)x+(y-n)y=3,即有x2+y2-mx-ny-3=0,求得圆心和半径,再由圆的最值的求法,即可得到所求|$\overrightarrow{c}$|范围.
解答 解:由|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|=2,
由向量的平行四边形法则,可得$\overrightarrow{a}⊥\overrightarrow{b}$,
设$\overrightarrow{a}$=(m,0),$\overrightarrow{b}$=(0,n),即有m2+n2=4,
∵|$\overrightarrow{a}$|≥1,∴m2≥1,则n2≤3,
∴|$\overrightarrow{b}$|的最大值是$\sqrt{3}$;
设$\overrightarrow{c}$=(x,y),由($\overrightarrow{c}$-$\overrightarrow{a}$)•($\overrightarrow{c}$-$\overrightarrow{b}$)=3,
可得(x-m)x+(y-n)y=3,
即有x2+y2-mx-ny-3=0,
表示圆心C($\frac{m}{2},\frac{n}{2}$),半径为$\sqrt{3+\frac{{m}^{2}+{n}^{2}}{4}}=2$的圆,
则|$\overrightarrow{c}$|=$\sqrt{{x}^{2}+{y}^{2}}$表示原点和圆上的点的距离,
即有最小值为2-$\sqrt{\frac{{m}^{2}+{n}^{2}}{4}}$=1;
最大值为2+$\sqrt{\frac{{m}^{2}+{n}^{2}}{4}}$=3.
∴|$\overrightarrow{c}$|的取值范围为[1,3].
故答案为:$\sqrt{3}$;[1,3].
点评 本题考查向量的数量积的坐标表示,考查坐标法的运用,圆的方程的运用,两点的距离的运用,属于中档题

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案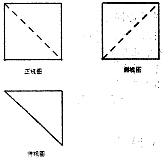 如图是某几何体的三视图,其中正视图、左视图均为正方形,俯视图是腰长为2的等腰三角腰形,则该几何体的体积是( )
如图是某几何体的三视图,其中正视图、左视图均为正方形,俯视图是腰长为2的等腰三角腰形,则该几何体的体积是( )| A. | $\frac{8}{3}$ | B. | $\frac{8}{3}$$\sqrt{2}$ | C. | $\frac{4}{3}$ | D. | 4 |
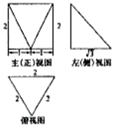
| A. | 12+$\sqrt{3}+\sqrt{7}$ | B. | 4+3$\sqrt{3}+\sqrt{7}$ | C. | 8+$\sqrt{3}+\sqrt{7}$ | D. | 4+$\sqrt{3}+\sqrt{7}$ |
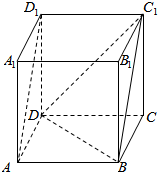 如图,在正方形ABCD-A1B1C1D1中,
如图,在正方形ABCD-A1B1C1D1中,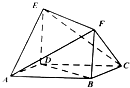 如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,∠BAD=$\frac{π}{3}$.
如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,∠BAD=$\frac{π}{3}$.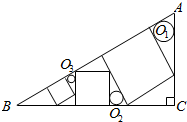 △ABC中,∠C=90°,作三个正方形及三个圆O1,O2,O3,如图,半径分别为r1,r2,r3.证明:r1r3=r${\;}_{2}^{2}$.
△ABC中,∠C=90°,作三个正方形及三个圆O1,O2,O3,如图,半径分别为r1,r2,r3.证明:r1r3=r${\;}_{2}^{2}$. 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E是PD的中点.
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=$\sqrt{2}$a,点E是PD的中点.