题目内容
5.已知函数f(x)=ex-$\frac{1}{2}{x^2}$-ax(a∈R).(Ⅰ)若函数f(x)的图象在x=0处的切线方程为y=2x+b,求a,b的值;
(Ⅱ)若函数f(x)≥1在$[\frac{1}{2},+∞)$上恒成立,求实数a的取值范围;
(Ⅲ)如果函数$g(x)=f(x)-(a-\frac{1}{2}){x^2}$恰有两个不同的极值点x1,x2,证明:$\frac{{{x_1}+{x_2}}}{2}$<ln(2a).
分析 (Ⅰ)求出原函数的导函数,由题意得到f′(0)=1-a,求出a值后代入原函数,再由f(0)=1求得b;
(Ⅱ)由题意知 $a≤\frac{{{e^x}-\frac{1}{2}{x^2}-1}}{x}$对$x≥\frac{1}{2}$恒成立,对函数$h(x)=\frac{{{e^x}-\frac{1}{2}{x^2}-1}}{x}$求导数,由导数可得h(x)在$(\frac{1}{2},+∞)$单增,得到$h(x)≥h(\frac{1}{2})=2\sqrt{e}-\frac{9}{4}$,则实数a的取值范围可求;
(Ⅲ)由已知$g(x)={e^x}-\frac{1}{2}{x^2}-ax-a{x^2}+\frac{1}{2}{x^2}={e^x}-a{x^2}-ax$,求其导函数,由x1,x2是函数g(x)的两个不同极值点(不妨设x1<x2),可得a>0,结合g′(x1)=0,g′(x2)=0得到${e^{x_1}}-2a{x_1}-a=0$,${e^{x_2}}-2a{x_2}-a=0$进一步得到$2a=\frac{{{e^{x_1}}-{e^{x_2}}}}{{{x_1}-{x_2}}}$,把问题转化为证明${e^{\frac{{{x_1}+{x_2}}}{2}}}<\frac{{{e^{x_1}}-{e^{x_2}}}}{{{x_1}-{x_2}}}$,变形为证$({x_1}-{x_2}){e^{\frac{{{x_1}-{x_2}}}{2}}}-{e^{{x_1}-{x_2}}}+1>0$,令x1-x2=t(t<0)换元.然后再利用导数证明$φ(t)=t{e^{\frac{t}{2}}}-{e^t}+1$φ(t)>0得答案.
解答 (Ⅰ)解:∵f′(x)=ex-x-a,
∴f′(0)=1-a,由题知1-a=2,解得a=-1.
∴$f(x)={e^x}-\frac{1}{2}{x^2}+x$.
∴f(0)=1,代入y=2x+b,得1=2×0+b,解b=1;
(Ⅱ)解:由题意知 $a≤\frac{{{e^x}-\frac{1}{2}{x^2}-1}}{x}$对$x≥\frac{1}{2}$恒成立,
令$h(x)=\frac{{{e^x}-\frac{1}{2}{x^2}-1}}{x}$,则$h'(x)=\frac{{(x-1){e^x}-\frac{1}{2}{x^2}+1}}{x^2}$,
令$m(x)=(x-1){e^x}-\frac{1}{2}{x^2}+1$,则m′(x)=x(ex-1),
当$x≥\frac{1}{2}$时,m′(x)>0,则m(x)在$(\frac{1}{2},+∞)$单增,$m(x)≥m(\frac{1}{2})=-\frac{1}{{2\sqrt{e}}}+\frac{7}{8}>0$,
∴h(x)在$(\frac{1}{2},+∞)$单增,则$h(x)≥h(\frac{1}{2})=2\sqrt{e}-\frac{9}{4}$.
故$a≤2\sqrt{e}-\frac{9}{4}$;
(Ⅲ)证明:由已知$g(x)={e^x}-\frac{1}{2}{x^2}-ax-a{x^2}+\frac{1}{2}{x^2}={e^x}-a{x^2}-ax$,
∴g′(x)=ex-2ax-a.
由x1,x2是函数g(x)的两个不同极值点(不妨设x1<x2),
∴a>0(若a≤0时,g′(x)>0,即g(x)是R上的增函数,与已知矛盾),
且g′(x1)=0,g′(x2)=0.
∴${e^{x_1}}-2a{x_1}-a=0$,${e^{x_2}}-2a{x_2}-a=0$.
两式相减得:$2a=\frac{{{e^{x_1}}-{e^{x_2}}}}{{{x_1}-{x_2}}}$,
于是要证明$\frac{{{x_1}+{x_2}}}{2}<ln2a$,即证明${e^{\frac{{{x_1}+{x_2}}}{2}}}<\frac{{{e^{x_1}}-{e^{x_2}}}}{{{x_1}-{x_2}}}$,
两边同除以${e^{x_2}}$,即证${e^{\frac{{{x_1}-{x_2}}}{2}}}<\frac{{{e^{{x_1}-{x_2}}}-1}}{{{x_1}-{x_2}}}$,即证$({x_1}-{x_2}){e^{\frac{{{x_1}-{x_2}}}{2}}}>{e^{{x_1}-{x_2}}}-1$,
即证$({x_1}-{x_2}){e^{\frac{{{x_1}-{x_2}}}{2}}}-{e^{{x_1}-{x_2}}}+1>0$,
令x1-x2=t(t<0).
即证不等式$t{e^{\frac{t}{2}}}-{e^t}+1>0$当t<0时恒成立.
设$φ(t)=t{e^{\frac{t}{2}}}-{e^t}+1$,
∴$ϕ'(t)={e^{\frac{t}{2}}}+t•{e^{\frac{t}{2}}}•\frac{1}{2}-{e^t}$=$(\frac{t}{2}+1){e^{\frac{t}{2}}}-{e^t}$=$-{e^{\frac{t}{2}}}[{e^{\frac{t}{2}}}-(\frac{t}{2}+1)]$.
而${e^{\frac{t}{2}}}>\frac{t}{2}+1$,即${e^{\frac{t}{2}}}-(\frac{t}{2}+1)>0$,∴φ′(t)<0,
∴φ(t)在(-∞,0)上是减函数.
∴φ(t)在t=0处取得极小值φ(0)=0.
∴φ(t)>0.
则$\frac{{{x_1}+{x_2}}}{2}<ln2a$.
点评 本题考查利用导数研究过曲线上某点处的切线的斜率,考查了导数在解决函数恒成立问题中的应用,训练了数学转化思想方法和函数构造法,是压轴题.

 阅读快车系列答案
阅读快车系列答案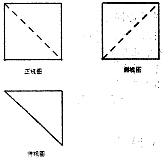 如图是某几何体的三视图,其中正视图、左视图均为正方形,俯视图是腰长为2的等腰三角腰形,则该几何体的体积是( )
如图是某几何体的三视图,其中正视图、左视图均为正方形,俯视图是腰长为2的等腰三角腰形,则该几何体的体积是( )| A. | $\frac{8}{3}$ | B. | $\frac{8}{3}$$\sqrt{2}$ | C. | $\frac{4}{3}$ | D. | 4 |
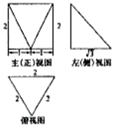
| A. | 12+$\sqrt{3}+\sqrt{7}$ | B. | 4+3$\sqrt{3}+\sqrt{7}$ | C. | 8+$\sqrt{3}+\sqrt{7}$ | D. | 4+$\sqrt{3}+\sqrt{7}$ |
| A. | 40° | B. | 40°或140° | C. | 140° | D. | 50° |
 如图,四边形ABCD是矩形,四边形BCEF是直角梯形,平面ABCD⊥平面BCEF,∠FBC是直角,AB=1,BC=BF=2,CE=4,P、Q、R分别是AF、DF、DE的中点.
如图,四边形ABCD是矩形,四边形BCEF是直角梯形,平面ABCD⊥平面BCEF,∠FBC是直角,AB=1,BC=BF=2,CE=4,P、Q、R分别是AF、DF、DE的中点.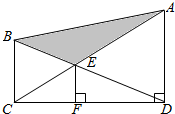 如图,直角梯形上、下底的和是14厘米,阴影部分面积是12平方厘米,EF是3厘米,求梯形面积.
如图,直角梯形上、下底的和是14厘米,阴影部分面积是12平方厘米,EF是3厘米,求梯形面积.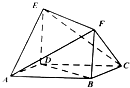 如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,∠BAD=$\frac{π}{3}$.
如图所示的多面体中,ABCD是菱形,BDEF是矩形,ED⊥面ABCD,∠BAD=$\frac{π}{3}$.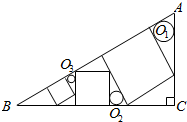 △ABC中,∠C=90°,作三个正方形及三个圆O1,O2,O3,如图,半径分别为r1,r2,r3.证明:r1r3=r${\;}_{2}^{2}$.
△ABC中,∠C=90°,作三个正方形及三个圆O1,O2,O3,如图,半径分别为r1,r2,r3.证明:r1r3=r${\;}_{2}^{2}$.