题目内容
15.如图是某三棱锥的三视图,则该三棱锥的表面积为( )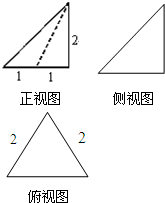
| A. | 4+$\sqrt{7}+\sqrt{3}$ | B. | 6+$\sqrt{7}$ | C. | 4+$\sqrt{7}$ | D. | 6+$\sqrt{3}$ |
分析 由已知中的三视图,可知该几何体是一个以俯视图为底面的三棱锥,分别求出各个面的面积,相加可得答案.
解答 解:由已知中的三视图,可知该几何体是一个以俯视图为底面的三棱锥,
其直观图如下图所示: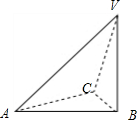
S△ABC=$\frac{\sqrt{3}}{4}×{2}^{2}$=$\sqrt{3}$,
S△VAB=S△VBC=$\frac{1}{2}$×2×2=2,
S△VCB=$\frac{1}{2}$×2×$\sqrt{(2\sqrt{2})^{2}-{1}^{2}}$=$\sqrt{7}$,
故该三棱锥的表面积为:4+$\sqrt{7}+\sqrt{3}$,
故选:A
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
相关题目
5.若a>b,则下列不等式成立的是( )
| A. | algx>blgx(x>0) | B. | ax2>bx2 | C. | a2>b2 | D. | $\frac{a}{{{2^x}+1}}>\frac{b}{{{2^x}+1}}$ |
7.用反证法证明命题:“三个连续正整数a,b,c中至少有一个能被2整除”时,要做的假设是( )
| A. | 假设三个连续正整数a,b,c都不能被2整除 | |
| B. | 假设三个连续正整数a,b,c都能被2整除 | |
| C. | 假设三个连续正整数a,b,c至多有一个能被2整除 | |
| D. | 假设三个连续正整数a,b,c至多有两个能被2整除 |