题目内容
【题目】在如图所示的四棱锥![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,
,![]() 为正三角形.
为正三角形.
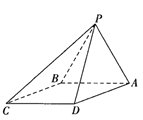
(1)证明:![]() ;
;
(2)若![]() ,四棱锥的体积为16,求
,四棱锥的体积为16,求![]() 的长.
的长.
【答案】(1)见解析(2)![]()
【解析】分析:(1)由正三角形的性质可得![]() ,
,![]() ,根据线面垂直的判定定理可得
,根据线面垂直的判定定理可得![]() 平面
平面![]() ,由线面垂直的性质可得结论;(2)根据勾股定理,
,由线面垂直的性质可得结论;(2)根据勾股定理,![]() ,结合
,结合![]() 可得,
可得,![]() 平面
平面![]() ,设
,设![]() ,利用棱锥的体积公式列方程解得
,利用棱锥的体积公式列方程解得![]() ,由勾股定理可得
,由勾股定理可得![]() 的长.
的长.
详解:(1)证明:取![]() 中点为
中点为![]() ,连接
,连接![]()
∵底面![]() 为菱形,
为菱形,![]() ,
,
∴![]() 为正三角形,
为正三角形,![]()
∴![]()
又∵![]() 为正三角形,
为正三角形,
∴![]()
又∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() .
.

(2)法一:设![]() ,则
,则![]() ,
,
在正三角形![]() 中,
中,![]() ,同理
,同理![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]()
∴![]()
∴![]() .
.
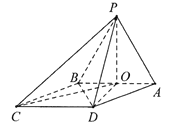
法二:设![]() ,则
,则![]() ,
,
在正三角形![]() 中,
中,![]() ,同理
,同理![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
∴![]() ,
,
连接![]() ,
,
∵在![]() 中,
中,![]() ,
,
∴由余弦定理得![]() ,
,
∴在![]() 中,
中,![]() .
.

练习册系列答案
相关题目
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.
元.
该公司将近![]() 天,每天揽件数量统计如下:
天,每天揽件数量统计如下:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
(1)某人打算将![]() ,
, ![]() ,
, ![]() 三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过
三件礼物随机分成两个包裹寄出,求该人支付的快递费不超过![]() 元的概率;
元的概率;
(2)该公司从收取的每件快递的费用中抽取![]() 元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过
元作为前台工作人员的工资和公司利润,剩余的作为其他费用.前台工作人员每人每天揽件不超过![]() 件,工资
件,工资![]() 元,目前前台有工作人员
元,目前前台有工作人员![]() 人,那么,公司将前台工作人员裁员
人,那么,公司将前台工作人员裁员![]() 人对提高公司利润是否更有利?
人对提高公司利润是否更有利?