题目内容
已知 是数列
是数列 前
前 项和,且
项和,且 ,对
,对 ,总有
,总有 ,则
,则 。
。
 是数列
是数列 前
前 项和,且
项和,且 ,对
,对 ,总有
,总有 ,则
,则 。
。
试题分析:当
 时,
时, ,(负舍),当
,(负舍),当 时,
时, ,所以
,所以 ,由
,由 ,所以
,所以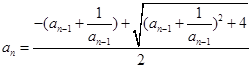 ,(负舍).由此归纳得:
,(负舍).由此归纳得: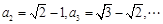 猜想
猜想 .因为
.因为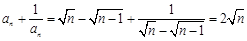 ,因此
,因此 ,所以由数学归纳法知猜想成立.
,所以由数学归纳法知猜想成立.
练习册系列答案
相关题目
题目内容
 是数列
是数列 前
前 项和,且
项和,且 ,对
,对 ,总有
,总有 ,则
,则 。
。
 时,
时, ,(负舍),当
,(负舍),当 时,
时, ,所以
,所以 ,由
,由 ,所以
,所以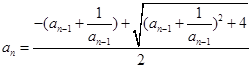 ,(负舍).由此归纳得:
,(负舍).由此归纳得: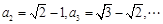 猜想
猜想 .因为
.因为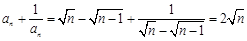 ,因此
,因此 ,所以由数学归纳法知猜想成立.
,所以由数学归纳法知猜想成立.