题目内容
已知数列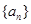 的前
的前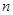 项和为
项和为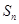 ,且
,且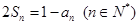 .
.
(1)求数列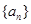 的通项公式;
的通项公式;
(2)设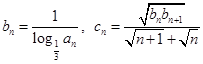 ,求数列
,求数列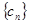 的前
的前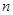 项和
项和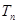 .
.
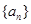 的前
的前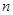 项和为
项和为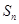 ,且
,且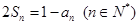 .
.(1)求数列
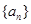 的通项公式;
的通项公式;(2)设
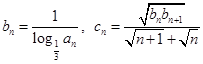 ,求数列
,求数列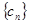 的前
的前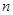 项和
项和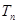 .
.(1)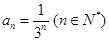 ;(2)
;(2)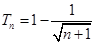 .
.
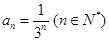 ;(2)
;(2)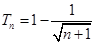 .
.试题分析:本题主要考查由
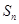 求
求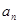 ,等比数列的通项公式、对数式的运算、裂项相消法求和等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,利用
,等比数列的通项公式、对数式的运算、裂项相消法求和等基础知识,考查学生的分析问题解决问题的能力、计算能力.第一问,利用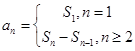 求通项,得到
求通项,得到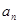 与
与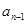 的关系式,根据等比数列的定义证明数列
的关系式,根据等比数列的定义证明数列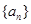 为等比数列,再利用等比数列的通项公式求
为等比数列,再利用等比数列的通项公式求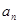 ;第二问,先利用对数式的公式化简
;第二问,先利用对数式的公式化简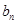 ,代入
,代入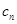 中再分离变量,利用裂项相消法求数列
中再分离变量,利用裂项相消法求数列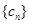 的前n项和
的前n项和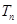 .
.(1)当
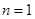 时,由
时,由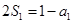 得:
得: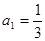 . 当
. 当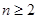 时,
时,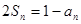 ① ;
① ;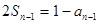 ② 上面两式相减,得:
② 上面两式相减,得: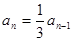 .
. 所以数列
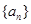 是以首项为
是以首项为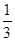 ,公比为
,公比为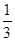 的等比数列. 得:
的等比数列. 得: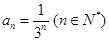 .……6分
.……6分(2)
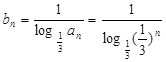
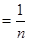 .
.  . ……10分
. ……10分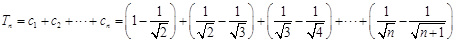
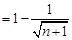 (12分)
(12分)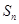 求
求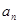 ,等比数列的通项公式、对数式的运算、裂项相消法求和.
,等比数列的通项公式、对数式的运算、裂项相消法求和.
练习册系列答案
相关题目
 }中,
}中, ,且
,且
 ,
, 的值;
的值; 是数列
是数列 前
前 项和,且
项和,且 ,对
,对 ,总有
,总有 ,则
,则 。
。 中,
中,
 是等比数列, 求实数
是等比数列, 求实数 ;
; 项和
项和 .
. (
(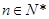 )那么
)那么 共有 项.
共有 项.