题目内容
已知等差数列{an}中,公差d>0,其前n项和为Sn,且满足:a2•a3=45,a1+a4=14.
(1)求数列{an}的通项公式;
(2)令bn=
,f(n)=
(n∈N*),求f(n)的最大值.
(1)求数列{an}的通项公式;
(2)令bn=
| 2Sn |
| 2n-1 |
| bn |
| (n+25)•bn+1 |
(Ⅰ)∵数列an}是等差数列,
∴a2•a3=45,a1+a4=a2+a3=14.
∴
或
.
∵公差d>0,
∴
,解得d=4,a1=1.
∴an=1+4(n-1)=4n-3.
(Ⅱ)∵Sn=na1+
=2n2-n,
∴bn=
=2n,
∴f(n)=
=
=
=
≤
=
=
.
当且仅当n=
,即n=5时,f(n)取得最大值
.
∴a2•a3=45,a1+a4=a2+a3=14.
∴
|
|
∵公差d>0,
∴
|
∴an=1+4(n-1)=4n-3.
(Ⅱ)∵Sn=na1+
| n(n-1)d |
| 2 |
∴bn=
| 2Sn |
| 2n-1 |
∴f(n)=
| bn |
| (n+25)•bn+1 |
| 2n |
| (n+25)?2(n+1) |
| n |
| n2+26n+5 |
| 1 | ||
n+
|
| 1 | ||||
26+2
|
| 1 |
| 26+10 |
| 1 |
| 36 |
当且仅当n=
| 25 |
| n |
| 1 |
| 36 |

练习册系列答案
相关题目
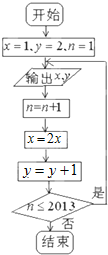
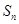 是数列
是数列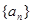 前
前 项和,且
项和,且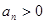 ,对
,对 ,总有
,总有 ,则
,则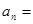 。
。