0＜x＜$\frac{1}{3}$.函数y=x的最大值为$\frac{1}{12}$．题目和参考答案——青夏教育精英家教网—

题目内容

7．0＜x＜$\frac{1}{3}$，函数y=x（1-3x）的最大值为$\frac{1}{12}$．

分析把函数y=x（1-3x）配方，根据自变量x的取值范围，求出y的最大值．

解答解：∵函数y=x（1-3x）
=-3x²+x
=-3${（x-\frac{1}{6}）}^{2}$+$\frac{1}{12}$；
且0＜x＜$\frac{1}{3}$，
∴当x=$\frac{1}{6}$时，y取得最大值，其最大值为$\frac{1}{12}$．
故答案为：$\frac{1}{12}$．

点评本题考查了二次函数在某一区间上的最值问题，是基础题目．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

18．设函数$f（x）=\left\{\begin{array}{l}x-[x]，x≤0\\ f（x-1），x＞0\end{array}\right.$，其中[x]表示不超过x的最大整数．若方程f（x）=ax有三个不同的实数根，则实数a的取值范围是（-1，-$\frac{1}{2}$]∪[$\frac{1}{4}$，$\frac{1}{3}$）．

15．在直角坐标系xoy中，“a＞b”是“方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1表示椭圆”的（　　）

	A．	充分而不必要条件		B．	必要而不充分条件
	C．	充要条件		D．	既不充分条件又不必要条件

2．已知两个正数a，b满足a+b=1
（1）求证：$\frac{1}{a}$+$\frac{1}{b}$≥4
（2）若不等式|x-2|+|2x-1|≤$\frac{1}{a}$+$\frac{1}{b}$对任意正数a，b都成立，求实数x的取值范围．

12．2015年安徽省文科高考数学试题考生一致认为比较简单，从而好成绩的取得不仅与知识掌握程度有关更与细节的把握程度有关（非知识错误）！学校就数学学科考试上是否有失误从本届文科毕业生中随机调查了100人，其中男生36人，有失误的学生中男生14人，女生16人．
（1）问：你有多大的把握认为细节的把握程度与性别有关？
（2）为了进一步调查考试中易犯哪些非知识错误，现用分层抽样的方法从100人中抽取样本容量为10的样本，求从这10人中任取两人，恰有一人犯有非知识错误的概率．
附：（1）临界值表：

p（k²≥k₀）	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k₀	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.828

（2）K²=$\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．

19．已知斜率为1的直线过椭圆$\frac{x^2}{4}+{y^2}$=1的焦点，且与椭圆交于A，B两点，则线段AB的长是$\frac{8}{5}$．

16．

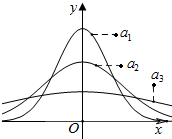如图分别是正态分布N（0，σ₁²），N（0，σ₂²），N（0，σ₃²）在同一坐标平面的分布密度曲线，则σ₁、σ₂、σ₃的大小关系为σ₁＜σ₂＜σ₃．

17．已知实数x，y满足条件$\left\{\begin{array}{l}{（x-3）^{2}+（y-2）^{2}≤1}\\{x-y-1≥0}\end{array}\right.$，则z=$\frac{y}{x-2}$的最小值为$\frac{3}{4}$．

试题分类