题目内容
【题目】（文）已知点D（1， 
）在双曲线C： 
=1（a＞0，b＞0）上，且双曲线的一条渐近线的方程是 
x+y=0．
（1）求双曲线C的方程；
（2）若过点（0，1）且斜率为k的直线l与双曲线C有两个不同交点，求实数k的取值范围；
（3）设（2）中直线l与双曲线C交于A、B两个不同点，若以线段AB为直径的圆经过坐标原点，求实数k的值．
【答案】
（1）解：由题知，有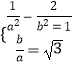 
解得 
因此，所求双曲线C的方程是 
（2）解：∵直线l过点（0，1）且斜率为k，
∴直线l：y=kx+1．
代入双曲线方程得（3﹣k2）x2﹣2kx﹣2=0．
又直线l与双曲线C有两个不同交点，
∴3﹣k2≠0且△=（﹣2k）2+8（3﹣k2）＞0
解得k∈（﹣ 
，﹣ 
）∪（﹣ ， ）∪（ ， ）
（3）解：设点A、B的坐标为（x1，y1）、（x2，y2）．
由（2）可得x1+x2= 
，x1x2= 
又以线段AB为直径的圆经过坐标原点，
则kOAkOB=﹣1，即x1x2+y1y2=0，
∴x1x2+（kx1+1）（kx2+1）=0，
即（k2+1）x1x2+k（x1+x2）+1=0，
∴ 
，解得k=±1．
又k=±1满足3﹣k2≠0且△=（﹣2k）2+8（3﹣k2）＞0，
∴所求实数k=±1
【解析】（1）点D（1， 
）代入双曲线方程，结合且双曲线的一条渐近线的方程是 x+y=0，建立方程，求出a，b，即可求双曲线C的方程；（2）直接联立直线与双曲线方程，化为关于x的一元二次方程，利用根的判别式，即可求实数k的取值范围；（3）存在实数k，使得以线段AB为直径的圆经过坐标原点转化为kOAkOB=﹣1，即x1x2+y1y2=0，整理后代入根与系数关系求解实数k的值．
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
相关题目
