Question

【题目】已知二次函数g（x）=mx2﹣2mx+n+1（m＞0）在区间[0，3]上有最大值4，最小值0．
（1）求函数g（x）的解析式；
（2）设f（x）= ．若f（2x）﹣k2x≤0在x∈[﹣3，3]时恒成立，求k的取值范围．

Answer 1

【答案】
（1）

解：∵g（x）=m（x﹣1）2﹣m+1+n

∴函数g（x）的图象的对称轴方程为x=1

∵m＞0依题意得 ，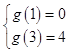

即 ，

解得

∴g（x）=x2﹣2x+1，

（2）

∵

∴ ，

∵f（2x）﹣k2x≤0在x∈[﹣3，3]时恒成立，

即 在x∈[﹣3，3]时恒成立

∴ 在x∈[﹣3，3]时恒成立

只需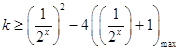

令 ，

由x∈[﹣3，3]得

设h（t）=t2﹣4t+1

∵h（t）=t2﹣4t+1

=（t﹣2）2﹣3

∴函数h（x）的图象的对称轴方程为t=2

当t=8时，取得最大值33．

∴k≥h（t）max=h（8）=33

∴k的取值范围为[33，+∞）

【解析】（Ⅰ）由题意得方程组解出即可，（Ⅱ）将f（x）进行变形，通过换元求出函数h（t）的最值，从而求出k的值．
【考点精析】认真审题，首先需要了解二次函数的性质(当时，抛物线开口向上，函数在上递减，在上递增；当时，抛物线开口向下，函数在上递增，在上递减)．