题目内容
8.已知数列{an}的通项公式为an=2n+(-1)n+1•(1+λn),其中是常数,n∈N*.(I)当a2=-1时,求λ的值;
(Ⅱ)数列{an}是否可能为等差数列?证明你的结论;
(Ⅲ)若对于任意n∈N*,都有an>0,求λ的取值范围.
分析 (I)通过在an=2n+(-1)n+1•(1+λn)中令n=2,计算即得结论;
(II)通过an=2n+(-1)n+1•(1+λn)(n∈N*)求出前4项的值,假设存在λ使{an}为等差数列,利用2a2=a1+a3可知λ=$-\frac{1}{2}$,验证即可得出结论;
(III)通过an>0可知(-1)n$•λ<2+\frac{{{{(-1)}^{n+1}}}}{n}$,分n为正奇数、正偶数两种情况讨论即可.
解答 解:(I)因为an=2n+(-1)n+1•(1+λn)(n∈N*),
所以n=2时,a2=3-2λ.(1分)
由3-2λ=-1,
解得λ=2.(2分)
(II)结论:数列{an}不可能为等差数列.
证明如下:
由an=2n+(-1)n+1•(1+λn)(n∈N*),得
a1=3+λ,a2=3-2λ,a3=7+3λ,a4=7-4λ.(4分)
若存在λ,使{an}为等差数列,则2a2=a1+a3,(5分)
即2(3-2λ)=(3+λ)+(7+3λ),
解得λ=$-\frac{1}{2}$.(6分)
于是,a2-a1=-3λ=$\frac{3}{2}$,a4-a3=-7λ=$\frac{7}{2}$,这与{an}为等差数列矛盾!
所以,对任意实数λ,{an}都不可能是等差数列.(7分)
(III)由an>0,得2n+(-1)n+1•(1+λn)>0,
将上式变形为(-1)n$•λ<2+\frac{{{{(-1)}^{n+1}}}}{n}$,其中n∈N*.①
(i)当n为正偶数时,①式化简为$λ<2-\frac{1}{n}$.
因为2-$\frac{1}{n}$随着正偶数n的增大而增大,
欲使上式对于任意正偶数恒成立,则λ<2$-\frac{1}{2}$=$\frac{3}{2}$.(9分)
(ii)当n为正奇数时,①式化简为$λ>-2-\frac{1}{n}$.
因为$-2-\frac{1}{n}$随着正奇数n的增大而增大,
欲使上式对于任意正奇数恒成立,则λ≥-2.(11分)
综上,若对于任意n∈N*,都有an>0,则λ的取值范围是[-2,$\frac{3}{2}$).(12分)
点评 本题考查数列的递推式,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案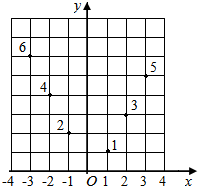 如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列$\left\{{a_n}\right\}({n∈{N^*}})$的前12项(如表所示),按如此规律下去,则a2015+a2016+a2017=( )
如图,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列$\left\{{a_n}\right\}({n∈{N^*}})$的前12项(如表所示),按如此规律下去,则a2015+a2016+a2017=( )| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 |
| x1 | y1 | x2 | y2 | x3 | y3 | x4 | y4 | x5 | y5 | x6 | y6 |
| A. | 1007 | B. | 1008 | C. | 1009 | D. | 2017 |
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
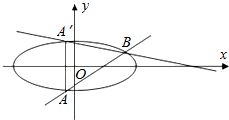 如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,短轴的一个端点到右焦点的距离为2.设直线l:x=my+1(m≠0)与椭圆C相交于A,B两点,点A关于x轴对称点为A′.
如图,已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{2}$,短轴的一个端点到右焦点的距离为2.设直线l:x=my+1(m≠0)与椭圆C相交于A,B两点,点A关于x轴对称点为A′.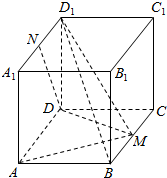 已知ABCD-A1B1C1D1是长方体,且AB=AA1=2,AD=4,M是BC中点,N是A1D1中点.
已知ABCD-A1B1C1D1是长方体,且AB=AA1=2,AD=4,M是BC中点,N是A1D1中点.