题目内容

3．设a∈R，n∈N*，求和：l+a+a2+a3+…+an=$\left\{\begin{array}{l}n+1，\;\;a=1\\ \frac{{1-{a^{n+1}}}}{1-a}，\;\;a≠1.\end{array}\right.$．

分析 分a=0、a=1、a≠0且a≠1分别求解得答案．

解答 解：当a=0时，l+a+a2+a3+…+an=0；
当a=1时，l+a+a2+a3+…+an=1+1+…+1=n+1；
当a≠0且a≠1时，l+a+a2+a3+…+an=$\frac{1-{a}^{n+1}}{1-a}$．
验证当a=0时，上式成立．
∴l+a+a2+a3+…+an=$\left\{\begin{array}{l}n+1，\;\;a=1\\ \frac{{1-{a^{n+1}}}}{1-a}，\;\;a≠1.\end{array}\right.$．
故答案为：$\left\{\begin{array}{l}n+1，\;\;a=1\\ \frac{{1-{a^{n+1}}}}{1-a}，\;\;a≠1.\end{array}\right.$．

点评 本题考查等比数列的前n项和，体现了分类讨论的数学思想方法，是基础题．

练习册系列答案
相关题目
13．若关于x的不等式|x-2|+|x-2a|＜6的解集不空，则a的取值范围是（-2，4）．
14．△ABC中，角A，B，C所对应的边分别为a，b，c，面积为S．
（1）若$\overrightarrow{AB}$•$\overrightarrow{AC}$=2$\sqrt{3}$S，求A的值；
（2）若tanA：tanB：tanC=1：2：3，且c=1，求b．
11．在直角坐标系内，到点（1，0）和直线x=-1距离相等的点的轨迹是曲线C
（1）求曲线C的方程．
（2）曲线C的焦点为F，问：是否存在过F且不垂直于x轴的直线l，使l与曲线C交于两点P，Q，并且△POQ的面积为2$\sqrt{2}$，并说明理由（O为原点）
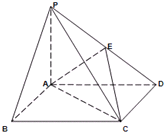18．如图，四棱锥P-ABCD中，底面ABCD为矩形，PA⊥底面ABCD，E为PD中点．
（1）求证：PB∥平面AEC；
（2）求证：平面PBC⊥平面PAB；
（3）设PA=1，AD=2，三棱锥P-ACD的体积V=$\frac{1}{3}$，求点A到平面PBC的距离．
8．已知数列{an}的通项公式为an=2n+（-1）n+1•（1+λn），其中是常数，n∈N*．
（I）当a2=-1时，求λ的值；
（Ⅱ）数列{an}是否可能为等差数列？证明你的结论；
（Ⅲ）若对于任意n∈N*，都有an＞0，求λ的取值范围．
15．已知f（x）=$\frac{1}{x}$，则f′（1）=（　　）
A．0B．1C．-1D．-2
12．给出下列四个命题：①当x＞0且x≠1时，有lnx+$\frac{1}{lnx}$≥2；②△ABC中，A＞B是sinA＞sinB成立的充要条件；
③函数y=ax的图象可以由函数y=2ax（其中a＞0且a≠1）的图象通过平移得到；④函数y=f（1+x）与函数y=f（1-x）的图象关于直线x=1对称；其中正确命题的序号为②③④．
5．设m，n是两条不同的直线，α，β，γ是三个不同的平面，则以下四个命题：
①$\left.\begin{array}{l}{α∥β}\\{α∥γ}\end{array}\right\}$⇒γ∥β②$\left.\begin{array}{l}{α⊥β}\\{m∥α}\end{array}\right\}$⇒m⊥β③$\left.\begin{array}{l}{m⊥α}\\{m∥β}\end{array}\right\}$⇒α⊥β④$\left.\begin{array}{l}{m∥n}\\{n⊆α}\end{array}\right\}$⇒m⊥α．
其中真命题为（　　）
A．①②B．②③C．①③D．②④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网