Question

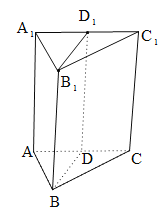
【题目】在三棱锥A﹣BCD中，△ABD和△ACD是边长为2的等边三角形，，O、E分别是BC、AC的中点．

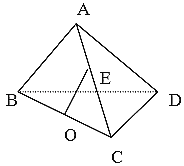
（1）求证：OE∥平面ABD；

（2）求证：平面ABC⊥平面BCD；

（3）求三棱锥A﹣BCD的表面积．

Answer 1

【答案】（1）见解析（2）见解析（3）4+2．

【解析】

（1）由O、E分别是BC、AC的中点，可得OE∥AB，由线面平行的判定定理可得OE∥平面ABD；

（2）连接AO，DO，可得AO⊥BC，DO⊥BC，可得∠AOD为二面角A﹣BC﹣D的平面角，由已知条件可得∠AOD＝90°，则平面ABC⊥平面BCD；

（3）分别计算出S△ABC、S△ABD、S△ACD、S△CBD，相加可得求三棱锥A﹣BCD的表面积．

（1）证明：O、E分别是BC、AC的中点，可得OE∥AB，

OE平面ABD，AB平面ABD，可得OE∥平面ABD；

（2）证明：连接AO，DO，

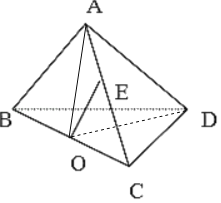
由AB＝AC＝BD＝DC＝2，可得AO⊥BC，DO⊥BC，

可得∠AOD为二面角A﹣BC﹣D的平面角，

由BC＝2，可得AO＝DO，

在△AOD中，AO2+DO2＝AD2，

可得∠AOD＝90°，

则平面ABC⊥平面BCD；

（3）三棱锥A﹣BCD的表面积为S△ABC+S△ABD+S△ACD+S△CBD2×222222×2＝4+2．