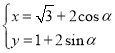题目内容
【题目】已知椭圆![]() 上任一点
上任一点![]() 到
到![]() ,
,![]() 的距离之和为4.
的距离之和为4.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)已知点![]() ,设直线
,设直线![]() 不经过
不经过![]() 点,
点,![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,若直线
两点,若直线![]() 的斜率与直线
的斜率与直线![]() 的斜率之和为
的斜率之和为![]() ,判断直线
,判断直线![]() 是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
是否过定点?若是,求出该定点的坐标;若不是,请说明理由.
【答案】(1)![]() ;(2)定点
;(2)定点![]() ,证明见解析
,证明见解析
【解析】
(1)根据椭圆的定义可得,![]() ,a=2,则b2=a2﹣c2=2,即可求得椭圆方程;
,a=2,则b2=a2﹣c2=2,即可求得椭圆方程;
(2)设直线l的方程,代入椭圆方程,根据韦达定理及直线的斜率公式化简可得m=﹣2k﹣4,再根据直线的点斜式方程,即可判断直线l恒过定点(2,﹣4).
(1)由椭圆定义知,![]() ,
,![]() ,
,
所以![]() ,
,
所以椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)直线l恒过定点(2,﹣4),理由如下:
若直线![]() 斜率不存在,则
斜率不存在,则![]() ,不合题意.
,不合题意.
故可设直线![]() 方程:
方程:![]() ,
,
联立方程组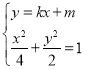 ,代入消元并整理得:
,代入消元并整理得:![]() ,
,
则![]() ,
,![]() .
.
![]() ,将直线方程代入,
,将直线方程代入,
整理得:![]() ,
,
即![]() ,
,
韦达定理代入上式化简得: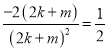 ,
,
因为![]() 不过
不过![]() 点,所以
点,所以![]() ,
,
所以![]() ,即
,即![]() ,
,
所以直线![]() 方程为
方程为![]() ,即
,即![]() ,
,
所以直线![]() 过定点
过定点![]() .
.

练习册系列答案
相关题目
【题目】某控制器中有一个易损部件,该部件由两个电子元件按图1方式连接而成.已知这两个电子元件的使用寿命(单位:小时)均服从正态分布![]() ,且各个元件能否正常工作相互独立.(一个月按30天算)
,且各个元件能否正常工作相互独立.(一个月按30天算)
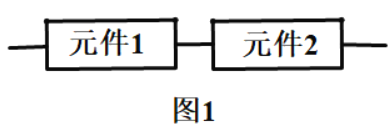
(1)求该部件的使用寿命达到一个月及以上的概率;
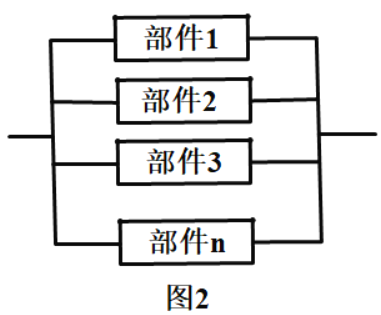
(2)为了保证该控制器能稳定工作,将若干个同样的部件按图2连接在一起组成集成块.每一个部件是否能正常工作相互独立.某开发商准备大批量生产该集成块,在投入生产前,进行了市场调查,结果如下表:
集成块类型 |
| 成本 | 销售金额 |
Ⅰ |
|
|
|
Ⅱ |
|
|
|
Ⅲ |
|
|
|
其中![]() 是集成块使用寿命达到一个月及以上的概率,
是集成块使用寿命达到一个月及以上的概率,![]() 为集成块使用的部件个数.报据市场调查,试分析集成块使用的部件个数为多少时,开发商所得利润最大?并说明理由.
为集成块使用的部件个数.报据市场调查,试分析集成块使用的部件个数为多少时,开发商所得利润最大?并说明理由.