Question

【题目】（本小题满分10分）【选修4-5：不等式选讲】

已知函数.

（Ⅰ）求的解集；

（Ⅱ）设函数， ，若对任意的都成立，求实数k的取值范围.

Answer 1

【答案】（1）或；（2）.

【解析】试题分析：本题主要考查绝对值不等式的解法、函数图象、恒成立问题等基础知识，考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问，先利用配方过程开方，得到绝对值不等式，利用零点分段法去掉绝对值符号，转化为不等式组，解不等式；第二问，将对任意的都成立，转化为，通过画分段函数图象和直线的图象，通过图形的位置关系得到结论.

试题解析：（Ⅰ） ，

∴，即， （2分）

∴① 或② 或③

解得不等式①：；②：无解；③： ，

所以的解集为或． （5分）

（Ⅱ）即的图象恒在图象的上方， （6分）

可以作出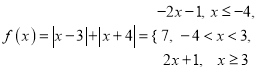的图象，

而图象为恒过定点，且斜率变化的一条直线，

作出函数图象如图3， （8分）

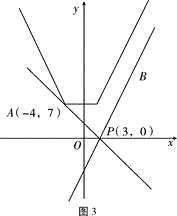
其中，∴，

由图可知，要使得的图象恒在图象的上方，

实数的取值范围应该为． （10分）