题目内容
(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分6分,
第3小题满分7分.
已知双曲线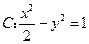 .
.
(1)求双曲线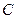 的渐近线方程;
的渐近线方程;
(2)已知点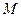 的坐标为
的坐标为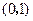 .设
.设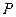 是双曲线
是双曲线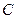 上的点,
上的点,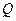 是点
是点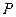 关于原点的对称点.
关于原点的对称点.
记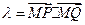 .求
.求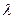 的取值范围;
的取值范围;
(3)已知点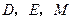 的坐标分别为
的坐标分别为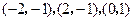 ,
,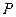 为双曲线
为双曲线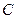 上在第一象限内的点.记
上在第一象限内的点.记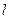 为经过原点与点
为经过原点与点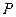 的直线,
的直线,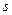 为
为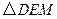 截直线
截直线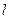 所得线段的长.试将
所得线段的长.试将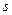 表示为直线
表示为直线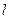 的斜率
的斜率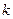 的函数.
的函数.
第3小题满分7分.
已知双曲线
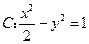 .
.(1)求双曲线
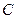 的渐近线方程;
的渐近线方程;(2)已知点
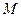 的坐标为
的坐标为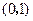 .设
.设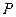 是双曲线
是双曲线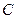 上的点,
上的点,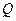 是点
是点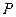 关于原点的对称点.
关于原点的对称点.记
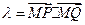 .求
.求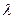 的取值范围;
的取值范围;(3)已知点
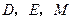 的坐标分别为
的坐标分别为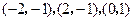 ,
,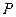 为双曲线
为双曲线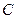 上在第一象限内的点.记
上在第一象限内的点.记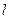 为经过原点与点
为经过原点与点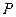 的直线,
的直线,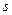 为
为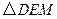 截直线
截直线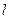 所得线段的长.试将
所得线段的长.试将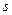 表示为直线
表示为直线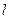 的斜率
的斜率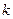 的函数.
的函数.(1)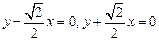
(2)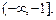
(3)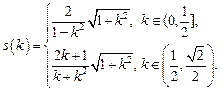
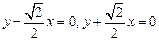
(2)
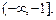
(3)
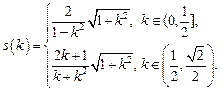
(1)所求渐近线方程为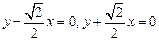 ……………...3分
……………...3分
(2)设P的坐标为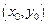 ,则Q的坐标为
,则Q的坐标为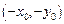 , …………….4分
, …………….4分
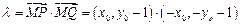
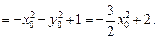 ……………7分
……………7分
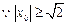
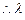 的取值范围是
的取值范围是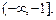 ……………9分
……………9分
(3)若P为双曲线C上第一象限内的点,
则直线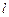 的斜率
的斜率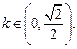 ……………11分
……………11分
由计算可得,当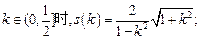
当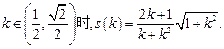 ……………15分
……………15分
∴ s表示为直线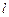 的斜率k的函数是
的斜率k的函数是
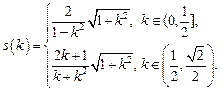 ….16分
….16分
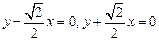 ……………...3分
……………...3分(2)设P的坐标为
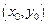 ,则Q的坐标为
,则Q的坐标为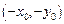 , …………….4分
, …………….4分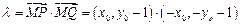
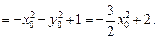 ……………7分
……………7分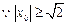
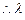 的取值范围是
的取值范围是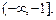 ……………9分
……………9分(3)若P为双曲线C上第一象限内的点,
则直线
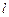 的斜率
的斜率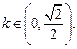 ……………11分
……………11分由计算可得,当
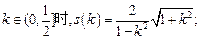
当
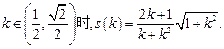 ……………15分
……………15分∴ s表示为直线
 的斜率k的函数是
的斜率k的函数是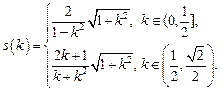 ….16分
….16分
练习册系列答案
相关题目
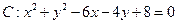 .以圆
.以圆 与坐标轴的交点分别作为双曲线的一个焦点和顶点,则适合上述条件的双曲线的标准方程为 .
与坐标轴的交点分别作为双曲线的一个焦点和顶点,则适合上述条件的双曲线的标准方程为 .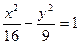 ,左焦点为
,左焦点为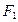 ,点
,点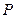 在双曲线右支上,求直线
在双曲线右支上,求直线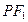 斜率范围
斜率范围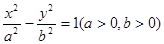 的离心率为
的离心率为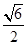 ,则双曲线的渐近线方程为
,则双曲线的渐近线方程为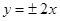 B.
B.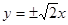 C.
C.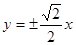 D.
D.
 有相同的渐近线且过点
有相同的渐近线且过点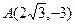 的双曲线方程是______。
的双曲线方程是______。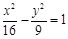 的焦距为
的焦距为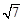
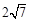
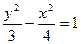 的渐近线方程是____________________。
的渐近线方程是____________________。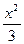 ―y2=1上两点,M为该双曲线右准线上一点,且
―y2=1上两点,M为该双曲线右准线上一点,且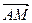 =
=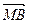 .
.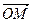 |的取值范围(O为坐标原点);
|的取值范围(O为坐标原点);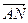 |=|
|=|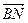 |总成立?并说明理由.
|总成立?并说明理由.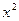 +4
+4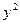 =16有相同的焦点,且一条渐近线为
=16有相同的焦点,且一条渐近线为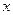 +
+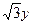 =0的双曲线的方程是: .
=0的双曲线的方程是: .