题目内容
22．（本小题满分12分）
A、B是双曲线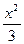
―y2=1上两点，M为该双曲线右准线上一点，且
=
．
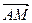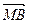（Ⅰ）求|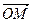
|的取值范围（O为坐标原点）；
（Ⅱ）是否存在定点N，使|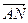
|＝|
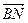|总成立？并说明理由．
A、B是双曲线
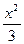―y2=1上两点，M为该双曲线右准线上一点，且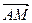=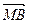．（Ⅰ）求|
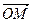|的取值范围（O为坐标原点）；（Ⅱ）是否存在定点N，使|
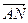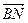|＝||总成立？并说明理由．
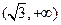，存在点（2，0）
练习册系列答案
相关题目
，存在点（2，0）题目内容
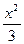―y2=1上两点，M为该双曲线右准线上一点，且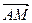=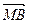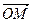．|的取值范围（O为坐标原点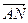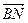）；|＝||总成立？并说明理由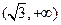．，存在点（2，0）
．
的渐近线方程；
的坐标为
．设
是双曲线
是点
．求
的取值范围；
的坐标分别为
，
为经过原点与点
为
截直线
的函数．
，
的顶点是该双曲线的中心，而焦点是其左顶点，求抛物线
在双曲线
的右支上，若点
到右焦点的距离等于
，则
.
的准线与双曲线
交于
、
两点，点
为抛物线的焦点，若
为直角三角形，则双曲线的离心率是 。
的一条渐近线
方程为
，则双曲线的离心率为（ ）
的离心率为 。
的左右焦点分别为
，
，点
在双曲线上，且
轴，若
，则双曲线的离心率等于（ ）
