题目内容
【题目】从含有两件正品
，
和一件次品
的3件产品中每次任取一件，连续取两次，求取出的两件产品中恰有一件是次品的概率．
（1）每次取出不放回；
（2）每次取出后放回．
【答案】（1）
（2）
【解析】
试题
(1)由题意列出所有可能的结果，共有6种，然后结合古典概型公式可得每次取出不放回的概率为
；
(2) 由题意列出所有可能的结果，共有9种，然后结合古典概型公式可得每次取出放回的概率为
；
试题解析：
（1）每次取出一个，取后不放回地连续取两次，其一切可能的结果组成的基本事件有6个，即
．用A表示“取出的两件中，恰好有一件次品”这一事件，则
.
（2）由题意知本题是一个古典概型，试验发生包含的事件是每次取出一个，取后放回地连续取两次，其一切可能的结果组成的基本事件有9个，即：
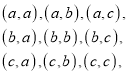
用B表示“取出的两种中，恰好有一件次品”这一事件，则
.
练习册系列答案
相关题目
【题目】如图，在三棱柱ABC–A1B1C1中，AB＝BC，D为AC的中点，O为四边形B1C1CB的对角线的交点，AC⊥BC1．求证：
（1）OD∥平面A1ABB1；
（2）平面A1C1CA⊥平面BC1D．
【题目】某电信公司从所在地的1000名使用4G手机用户中，随机抽取了20名，对其收集每日使用流量（单位：M）进行统计，得到如下数据：
流量x | 0≤x＜5 | 5≤x＜10 | 10≤x＜15 | 15≤x＜20 | 20≤x＜25 | x≥25 |
人数 | 1 | 6 | 6 | 5 | 2 | 0 |
（1）估计这20名4G手机用户每日使用流量（单位：M）的平均值；
（2）估计此地1000名使用4G手机用户中每日使用流量不少于10M用户数；
（3）在15≤x＜20和20≤x＜25两组用户中，随机抽取两人作进一步问卷调查，求所抽取的两人恰好来自不同组的概率．
