题目内容
【题目】如图,过点P作圆O的割线PBA与切线PE,E为切点,连接AE、BE,∠APE的平分线与AE、BE分别交于点C、D,其中∠AEB=30°. 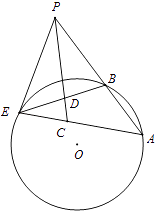
(1)求证: ![]()
(2)求∠PCE的大小.
【答案】
(1)证明:∵PE是圆的切线,∴∠PEB=∠PAC,
∵AE是∠APE的平分线,∴∠EPC=∠APC,
∴△PED∽△PAC,
∴ ![]() =
= ![]() ,
,
∵ ![]() =
= ![]() ,
,
∴ ![]()
(2)解:∵PE是圆的切线,∴∠PEB=∠PAC,
∵AE是∠APE的平分线,∴∠EPC=∠APC,
根据三角形的外角与内角关系有:∠EDC=∠PEB+∠EPC;∠ECD=∠PAC+∠APC,
∴∠EDC=∠ECD,∴△EDC为等腰三角形,
又∠AEB=30°,
∴∠EDC=∠ECD=75°,即∠PCE=75°
【解析】(1)证明△PED∽△PAC,结合角平分线的性质,即可证明结论;(2)利用PE是圆的切线,可得∠PEB=∠PAC,利用AE是∠APE的平分线,可得∠EPC=∠APC,根据三角形的外角与内角关系,可得∠EDC=∠ECD,即可得出结论.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某电信公司从所在地的1000名使用4G手机用户中,随机抽取了20名,对其收集每日使用流量(单位:M)进行统计,得到如下数据:
流量x | 0≤x<5 | 5≤x<10 | 10≤x<15 | 15≤x<20 | 20≤x<25 | x≥25 |
人数 | 1 | 6 | 6 | 5 | 2 | 0 |
(1)估计这20名4G手机用户每日使用流量(单位:M)的平均值;
(2)估计此地1000名使用4G手机用户中每日使用流量不少于10M用户数;
(3)在15≤x<20和20≤x<25两组用户中,随机抽取两人作进一步问卷调查,求所抽取的两人恰好来自不同组的概率.
【题目】为了调查喜欢看书是否与性别有关,某校调查小组就“是否喜欢看书”这个问题,在全校随机调研了100名学生.
(1)完成下列![]() 列联表:
列联表:
喜欢看书 | 不喜欢看书 | 合计 | |
女生 | 15 | 50 | |
男生 | 25 | ||
合计 | 100 |
(2)能否在犯错率不超过0.025的前提下认为“喜欢看书与性别有关”.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5024 | 6.635 | 7.879 | 10.828 |
(参考公式:![]() ,其中
,其中![]() )
)