题目内容
设函数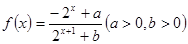 .
.
(1)当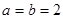 时,证明:函数
时,证明:函数 不是奇函数;
不是奇函数;
(2)设函数 是奇函数,求
是奇函数,求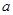 与
与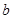 的值;
的值;
(3)在(2)条件下,判断并证明函数 的单调性,并求不等式
的单调性,并求不等式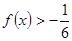 的解集.
的解集.
(1)详见解析;(2)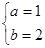 ;(3)
;(3)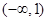 .
.
解析试题分析:(1)当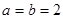 时,
时, ,函数的定义域为
,函数的定义域为 ,要证明函数不是奇函数,从奇函数的定义出发,可考虑选一个特殊值
,要证明函数不是奇函数,从奇函数的定义出发,可考虑选一个特殊值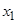 ,满足
,满足 ,若
,若 最简单;(2)由函数是奇函数,则有对函数定义域内的任意一个
最简单;(2)由函数是奇函数,则有对函数定义域内的任意一个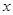 ,都满足
,都满足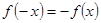 ,由此等式恒成立可得关于
,由此等式恒成立可得关于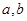 的等式求出
的等式求出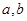 ,也可先用特殊数值求出
,也可先用特殊数值求出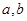 ,再进行检验;(3)先判断函数的单调性,再用定义法或导数法证明,再解不等式,解不等式时可直接求解,也可利用函数单调性求解.
,再进行检验;(3)先判断函数的单调性,再用定义法或导数法证明,再解不等式,解不等式时可直接求解,也可利用函数单调性求解.
试题解析:(1)当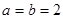 时,
时,
由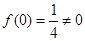 ,知函数
,知函数 不是奇函数.
不是奇函数.
(2)由函数 是奇函数,得
是奇函数,得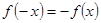 ,
,
即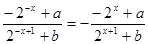 对定义域内任意实数
对定义域内任意实数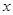 都成立,化简整理得
都成立,化简整理得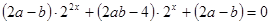 对定义域内任意实数
对定义域内任意实数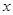 都成立
都成立
所以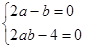 ,所以
,所以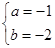 或
或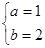
经检验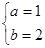 符合题意.
符合题意.
(3)由(2)可知
易判断 为R上的减函数,证明如下:
为R上的减函数,证明如下:
因为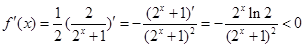 ,所以
,所以 为R上的减函数;
为R上的减函数;
由 ,不等式
,不等式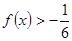 即为
即为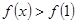 ,由
,由 在R上的减函数可得
在R上的减函数可得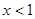 ,
,
所以不等式的解集为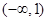 .
.
另解:由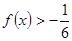 得,即
得,即 ,解得
,解得 ,所以
,所以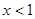 .
.
(注:若没有证明 的单调性,直接解不等式,正确的给3分)
的单调性,直接解不等式,正确的给3分)
考点:函数的的单调性和奇偶性.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
 ,
,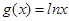 .
. 在
在 上是单调减函数,求
上是单调减函数,求 的取值范围;
的取值范围; ,使得方程
,使得方程 在区间
在区间 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出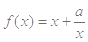 ,且
,且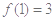 .
.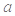 的值,并确定函数
的值,并确定函数 的定义域;
的定义域;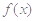 在
在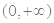 范围内的单调性;
范围内的单调性;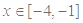 时,求出函数
时,求出函数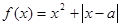 (
(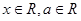 ).
). 的奇偶性;
的奇偶性;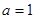 时,求
时,求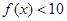 对
对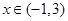 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 是定义在
是定义在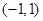 上的奇函数,且
上的奇函数,且 .
. 为奇函数.
为奇函数. ,试判断
,试判断 的单调性(不需证明);
的单调性(不需证明); ,使
,使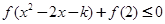 ,求实数k的最大值.
,求实数k的最大值.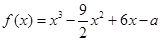 .
.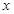 ,
,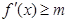 恒成立,求
恒成立,求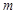 的最大值;
的最大值;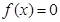 有且仅有一个实根,求
有且仅有一个实根,求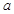 的取值范围.
的取值范围. 是定义在
是定义在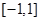 上的奇函数,且
上的奇函数,且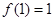 ,若
,若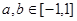 ,
,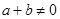 有
有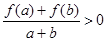 恒成立.
恒成立.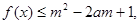 对所有
对所有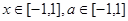 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。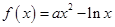 (
( 为常数).
为常数).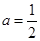 时,求
时,求 的单调递减区间;
的单调递减区间;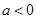 ,且对任意的
,且对任意的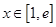 ,
,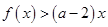 恒成立,求实数
恒成立,求实数