题目内容
10.设A⊆Z,A≠∅,从A到Z的两个函数分别为f(x)=x2+1,g(x)=3x+5.若?x∈A,都有 f(x)=g(x),则满足条件的集合A的个数为3.分析 令x2+1=3x+5.解得:x=-1,或x=4,进而可列举出满足条件的集合A.
解答 解:令x2+1=3x+5.
解得:x=-1,或x=4,
故当A={-1},A={4},A={-1,4}时满足条件,
故满足条件的集合A的个数为3个,
故答案为:3.
点评 本题考查的知识点是集合的子集,其中找到满足条件的A必为{-1,4}的非空子集,是解答的关键.

练习册系列答案
相关题目
1.演绎推理“因为指数函数y=ax(a>0,a≠1)是增函数,而函数y=0.5x是指数函数,所以y=0.5x是增函数”,所得结论错误的原因是( )
| A. | 大前提错误 | B. | 小前提错误 | ||
| C. | 推理形式错误 | D. | 大前提与小前提均错误 |
15. 运行如图所示的程序框图,若输出结果为$\frac{6}{7}$,则判断框中应该填的条件是( )
运行如图所示的程序框图,若输出结果为$\frac{6}{7}$,则判断框中应该填的条件是( )
 运行如图所示的程序框图,若输出结果为$\frac{6}{7}$,则判断框中应该填的条件是( )
运行如图所示的程序框图,若输出结果为$\frac{6}{7}$,则判断框中应该填的条件是( )| A. | k>5 | B. | k>6 | C. | k>7 | D. | k>8 |
2.执行下面的程序框图,则输出的m的值为( )


| A. | 9 | B. | 7 | C. | 5 | D. | 11 |
20.已知数列{an}满足a2=34,an+1-an=4n(n∈N*),则数列{$\frac{{a}_{n}}{n}$}的最小值是( )
| A. | 15 | B. | 14 | C. | $\frac{27}{2}$ | D. | 16 |


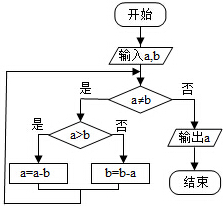 如图,该程序框图的算法思路源于我国古代数学专著《九章算术》中的“更相减损术”,执行此程序框图,若输入的m,n分别为72,168,则输出的m=( )
如图,该程序框图的算法思路源于我国古代数学专著《九章算术》中的“更相减损术”,执行此程序框图,若输入的m,n分别为72,168,则输出的m=( )