题目内容
19.化简再求值:$({\frac{a^2}{{{a^2}+2ab+{b^2}}}-\frac{a}{a+b}})÷({\frac{a^2}{{{a^2}-{b^2}}}-\frac{b}{a-b}-1})$,其中a=$\sqrt{3}$+2,b=$\sqrt{3}$-2.分析 通分化简代入即可得出.
解答 解:$({\frac{a^2}{{{a^2}+2ab+{b^2}}}-\frac{a}{a+b}})÷({\frac{a^2}{{{a^2}-{b^2}}}-\frac{b}{a-b}-1})$=$\frac{{a}^{2}-a(a+b)}{(a+b)^{2}}$×$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-b(a+b)-({a}^{2}-{b}^{2})}$
=$\frac{-ab}{a+b}$×$\frac{a-b}{-ab}$
=$\frac{a-b}{a+b}$,
又a=$\sqrt{3}$+2,b=$\sqrt{3}$-2.
∴原式=$\frac{(\sqrt{3}+2)-(\sqrt{3}-2)}{(\sqrt{3}+2)+(\sqrt{3}-2)}$
=$\frac{4}{2\sqrt{3}}$
=$\frac{2\sqrt{3}}{3}$.
点评 本题考查了代数式的化简求值、乘法公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
9.阅读程序框图,如果输出i=5,那么在空白矩形框中填入的语句为( )
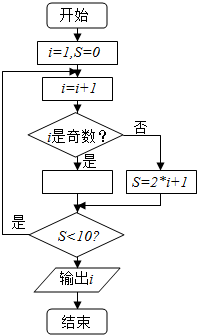

| A. | S=2*i+4 | B. | S=2*i-1 | C. | S=2*i-2 | D. | S=2*i |
14.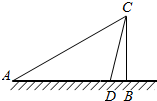 如图,某人欲测量某建筑物的高度BC,在A处测得建筑物顶端C的仰角为30°,然后,向建筑物方向前进200m到达D处,在D处测得C的仰角为75°,则建筑物的高度为( )
如图,某人欲测量某建筑物的高度BC,在A处测得建筑物顶端C的仰角为30°,然后,向建筑物方向前进200m到达D处,在D处测得C的仰角为75°,则建筑物的高度为( )
 如图,某人欲测量某建筑物的高度BC,在A处测得建筑物顶端C的仰角为30°,然后,向建筑物方向前进200m到达D处,在D处测得C的仰角为75°,则建筑物的高度为( )
如图,某人欲测量某建筑物的高度BC,在A处测得建筑物顶端C的仰角为30°,然后,向建筑物方向前进200m到达D处,在D处测得C的仰角为75°,则建筑物的高度为( )| A. | 50($\sqrt{3}$+1)m | B. | 50($\sqrt{2}$+1)m | C. | 50($\sqrt{3}$-1)m | D. | 50($\sqrt{3}$+$\sqrt{2}$) m |
