题目内容
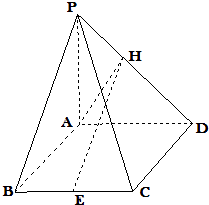
【题目】如图,已知四棱锥P﹣ABCD中,底面ABCD是棱长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC中点,若H为PD上的动点,EH与平面PAD所成最大角的正切值为 ![]() .
. 
(1)当EH与平面PAD所成角的正切值为 ![]() 时,求证:EH∥平面PAB;
时,求证:EH∥平面PAB;
(2)在(1)的条件下,求二面角A﹣PB﹣C的余弦值.
【答案】
(1)证明:连接AC,由题设知△ABC为正三角形,所以AE⊥BC,
又BC∥AD,因此AE⊥AD;
∵PA⊥平面ABCD,AE平面ABCD,
∴PA⊥AE
而PA平面PAD,AD平面PAD,且PA∩AD=A,
所以AE⊥平面PAD,
则∠EHA为EH与平面PAD所成的角.
在Rt△EAH中,AE= ![]()
所以当AH最短时,∠EHA最大;
即当AH⊥PD时,∠EHA最大;
此时tan∠EHA= ![]() =
= ![]() =
= ![]() ,
,
因此AH= ![]() ,
,
又AD=2,∴∠ADH={45°}∴PA=2
∴H为PD的中点,
取PA的中点M,连接HM,MB,则HM= ![]() 且HM∥AD,DB=
且HM∥AD,DB= ![]() AD且DB∥AD,
AD且DB∥AD,
∴HM∥DB且HM=DB
∴四边形DHMB为平行四边形
∴EH∥BM,
又BM平面PAB
∴EH∥平面PAB
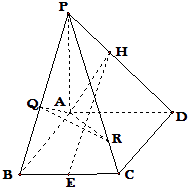
(2)解:∵PA⊥面ABCD,PA平面PAB,
∴平面PAB⊥平面ABCD,
∵PB面PAB∴CM⊥PB,
∴PB⊥面CQM,∴ ![]() ,
,
∴△ABC为正三角形,∴点M为AB的中点,
∴ ![]() ,∴
,∴ ![]() ,
,
∴ 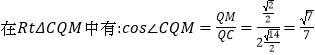
【解析】(1)首先要证明AE⊥平面PAD,则∠EHA为EH与平面PAD所成的角;所以当AH最短时,∠EHA最大;即当AH⊥PD时,∠EHA最大;接着利用构造平行四边形法判定线面平行即可;(2)利用已知条件证明平面PAB⊥平面ABCD,PB⊥面CQM,所求二面角转化到Rt△CQM中即可;
【考点精析】利用直线与平面平行的判定对题目进行判断即可得到答案,需要熟知平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.