题目内容
已知两条异面直线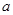 、
、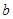 ,
,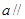 平面
平面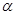 ,则
,则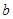 与
与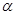 的位置关系是( )
的位置关系是( )
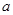 、
、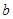 ,
,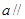 平面
平面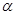 ,则
,则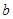 与
与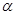 的位置关系是( )
的位置关系是( )A.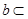 平面 平面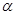 | B.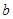 与平面 与平面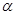 相交 相交 | C.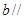 平面 平面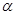 | D.以上都有可能 |
D
 |
如图:长方体ABCD—EFGH,平面
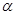 是平面ABCD,EH=a,则直线b可能是AB、AE、FG;故选D
是平面ABCD,EH=a,则直线b可能是AB、AE、FG;故选D
练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目
题目内容
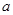 、
、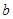 ,
,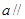 平面
平面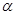 ,则
,则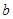 与
与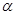 的位置关系是( )
的位置关系是( )A.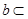 平面 平面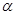 | B.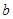 与平面 与平面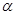 相交 相交 | C.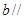 平面 平面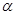 | D.以上都有可能 |
 |
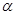 是平面ABCD,EH=a,则直线b可能是AB、AE、FG;故选D
是平面ABCD,EH=a,则直线b可能是AB、AE、FG;故选D
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案